大家好!我是小麦。不知道大家有没有这样的经历:做选择题的时候就在最后两个选项纠结,结果经常因为坚持原来的选项,选错了答案,而如果当时改了答案的话,基本都能选对(毕竟还有瞎蒙这种情况==)。而经过和他人讨论后,发现这种情况似乎并不在少数。这其中难道隐藏着什么玄机吗?
要解决这样的问题,Master X给了我一个小课题研究,不妨先来了解一下:
蒙提霍尔问题
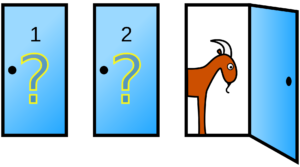
蒙提霍尔问题(Monty Hall Problem),又叫三门问题。大致出自美国的电视游戏节目Let's Make a Deal。问题名字来自该节目的主持人蒙提·霍尔(Monty Hall)。参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。
那么现在问题就是:换另一扇门会否增加参赛者赢得汽车的概率?
你可能会想:之前三个门中选中汽车的概率是\frac{1}{3}, 现在开了一扇门去掉了一个错误答案,只剩下两个门,那么选到汽车的概率不就是\frac{1}{2} 吗?
然而在参与者当中,坚持原先选项获得汽车的人几乎为更改后获得汽车的人数的一半。也就是说,更改后获得汽车的概率可理解为\frac{2}{3}.
这一事件引起了当时许多学者的讨论,甚至有人因为提出了概率不是\frac{1}{2}而被众多博士争议、抱怨。
虽然该问题的答案在逻辑上并不自相矛盾,但十分违反直觉。
那么事实究竟是什么呢?我们先不用数学方法考虑,进行穷举。
穷举证明
假设在三个门后面,分别有山羊一,山羊二,汽车。
如果一开始选的门后面是山羊一,那么主持人打开山羊二的门,此时换门可以获得汽车
如果一开始选的门后面是山羊二,那么主持人打开山羊一的门,此时换门可以获得汽车
如果一开始选的门后面是汽车,那么主持人打开山羊一或山羊二的门,此时不换门可以获得汽车
此时,换门获得汽车的比例为\frac{2}{3}
接下来,我们进行简单的概率说明:
第一次选中山羊的概率为\frac{2}{3},之后主持人开另一个空门,换门,得到汽车。事件总概率2/3。
第一次选中汽车的概率为\frac{1}{3},之后主持人随机开一个门(\frac{1}{2}),这两个门都有可能被选中,总概率为\frac{1}{3}\times\frac{1}{2}\times2=\frac{1}{3}。
当然还可以使用贝叶斯定理进行证明。
贝叶斯定理证明
我们首先设定以下三个随机事件:
A:所选的X号门后是汽车。
B:换门后,当前门后是汽车
C:你选择了X号门,而主持人打开了y号门并且y号门后面是山羊。
如果坚持不换门的情况下,我们的目标是P(A|C),即在得到主持人信息之后1号门后是汽车的概率。在主持人提供信息之前,我们有P(A)=\frac{1}{3}。
D发生的几率,仔细想想是\frac{1}{2},因为主持人会随机的打开一扇门后有羊的门。
这个地方的\frac{1}{2}\times\frac{2}{3}=\frac{1}{2}\times\frac{1}{3}+\frac{1}{2}\times\frac{1}{3}
换门的话,我们的目标是P(B|C), 此时P(C)的概率就变成了1,是必然事件了
根据贝叶斯公式就可求得结果是\frac{2}{3}
得证。
分析
为什么会造成这样一种现象呢?小麦认为,问题出现在主持人上。主持人始终都知道门后是什么,换句话说他一定能排除掉一个选项。而这个行为是建立在已经做出了选择的基础上的。
怎么理解,我们分析这样一个问题:
“参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。
此时把原先参赛者换下,换来了一位新的参赛者,主持人会问新参赛者选之前选的那扇还是剩下的那扇。”
你可以发现,其实问题并没有变化,概率还是之前的\frac{2}{3}。可是在新的参赛者眼里,他觉得就是两个门,其中有个门中有汽车,所以概率是\frac{1}{2}。他的理解并没有错误,因为这是建立在他已有的消息基础上的,他只知道去掉了一个选项,不知道之前所发生的一切,所以产生了概率是\frac{1}{2}的认知。而概率是不会随主观认识而变化的。
扩展研究
我将我的思考和Master X分享后,Master X认可了我的想法,并且提出了他的想法:
概率存在于被给予的条件下,而不能寄托在实际的物体上。
就好比抛硬币,抛出正反面\frac{1}{2}的概率本质上是建立在重复实验+大数定理得来的。如果要较真的话,“真实"的概率应该要考虑硬币本身的材质和每一面的图案分布,而我们在看待这一问题时是建立在忽略这些条件上的。
同时Master X和我探讨了本次研究蒙提霍尔问题的收获:
在现实生活中,如果你在做某件事可采取的三种方式中选择了A方式,而另一个人采取了B方式失败了,那么不如采取C方式成功的可能性更高。并且可选选项越多,排除掉的选项越多,换了后成功的概率也就越大。
那么现在回到我们的标题上,如何把选择题做对的概率由1/4提高到3/4呢?(划重点)
按以下步骤执行:
首先,在备选的四个选项中等可能地选择一个备选选项,先不要考虑它的对错。
然后,在剩下三个选项中保证自己能去掉两个错误选项(在知识得以保证的情况下,这是肯定可以做到的。当然在这一步可能你会遇到真正的正确答案,但请不要急着选择,留待验证)
接着,将原先的备选选项和剩下的选项进行比较。如果不确定的话,选择后者做对的概率是3/4。当然你也可以自己验证,选出正确答案。
以上步骤经过验证,符合逻辑分析结果,但有以下注意事项:
1.最初的选择必须做到等可能,你可以理解为不看选项的情况下随意选择,而不是一眼看出某个选项是错的而不选它。
2.不要在去掉两个错误选项时看到一个貌似正确的就退出,因为存在你知识量不足去不掉两个选项的情况
3.请注意最后换了对的概率是75%而不是100%,也就是说没和你打包票换了一定对,没换一定错
4.这个方法不能反向推理!你可能会认为在做完了之后,如果我一开始选的是剩下的选项,而剩下原先备选的选项,那概率不就反过来矛盾了吗?首先请参考第三条注意点,其次你做出这种判断的原因是建立在已经做了一次的原因上的。请再次理解Master X的这句话:概率存在于被给予的条件下,而不能寄托在实际的物体上。不要认为正确答案的概率从始至终就比错误答案概率大。
课后思考
看完了以上的内容,如果你还有点晕/感兴趣的话,不妨思考下面这个问题:
有三个方框:
1.一个装有两枚金币的盒子,
2.一个装有两枚银币的盒子,
3.一个装有一枚金币和一枚银币的盒子
在随机选择一个盒子并随机取出一枚硬币之后,如果恰好是一枚金币,则从同一个盒子中取出的下一枚硬币也是一枚金币的概率是多少?
这个问题被称为Bertrand's box paradox,你可以自行查询验证,答案是2/3。


文章评论