开个新坑笔记整理系列,目前主要以社交网络方向为主,不定期更新,干货比较多,内容应该是会越写越多的,想到哪补到哪吧……
作为图系列的第一章,本文将从图表征学习这条脉络线开始讲起。
在正式开始内容之前,按照惯例先补充一些必要的说明。
基本单位为节点和连边,以节点代表实体,连边代表节点间存在关系的一种描述形式,可写成 G=(V,E) 。
其中节点作为实体可以存储实体的信息,而根据连边是否具有方向可将图分为有向图和无向图,是否具有权重可分为带权图和无权图。
在社交网络中每名用户就可以看成是实体,用户间的关系可以看成是连边,因此社交网络常可以建模为图的问题进行研究。
除了点和边外,常用的图相关信息为度 D 和邻接矩阵 A\in R^{ |V|\times |V|}。
比较公认的有代表性的追溯起源为Bengio的Representation Learning: A Review and New Perspectives(记得引用),概论性地讲述了表征学习的定义和意义:简单来说,机器学习的成功很大一部分取决于数据的表达好坏(特征工程:√),不同的表达会使同样的信息混淆或者隐藏,更何况部分任务(NLP中尤其常见)所处理的信息并非易于处理和表达的形式(如声音、文字),因此这些信息需要尽可能用相对易处理的形式表达。尽管特定的领域知识可以有助于设计或者选择数据的表达,但通过一般的先验知识来学习表达也是有效的。因此,表征学习是通过学习的方式,将所处理的信息采用易于处理形式表达的一种数据预处理的工作。
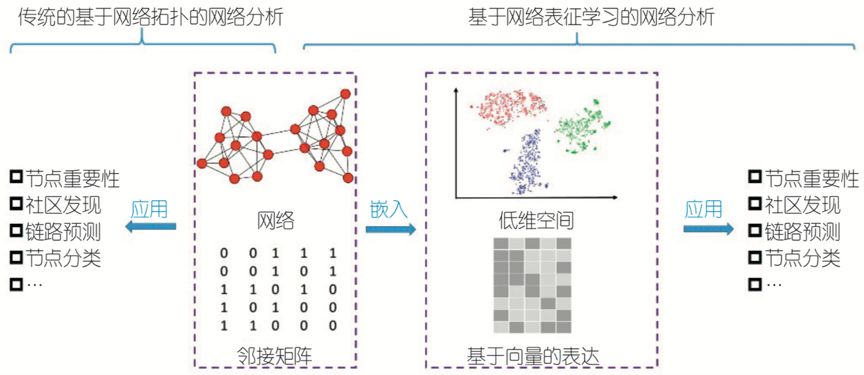
那么具体到我们图上的任务,由于图自身特性存储了大量的信息,而图本身的拓扑形式使得其难以直接处理,因此我们需要将其转换成一种易于计算机(或者说机器学习模型输入)处理的数据形式,例如向量、矩阵。
那么你可能发现了,诶邻接矩阵不就是一种将图用矩阵存储表达的数据形式吗?它包含了除节点内部信息外图的全部原始信息并且没有损失,这不就是一种图的表征形式吗?
没错,此贴终结。这是个很好的问题。恭喜你,当你能思考到这个层面的时候,接下来的内容就很好理解了。
答案是,是也不是。
事实上,在本文后续图表征学习正式进入机器学习时代前,邻接矩阵就是图的常用表征形式,甚至在后面论文实验所对比的算法都是传统的对邻接矩阵直接处理的算法(如谱聚类、拉普拉斯矩阵分解)。但是它的缺点也很明显:
1)存储空间太大。邻接矩阵所需的空间为 |V|\times |V| ,对于社交网络来说,用户一旦达到万级甚至百万级别,处理起来将是灾难级的任务。此外,由于大量节点间不存在连边,对于稀疏图来说,有大量的空间被浪费。
2)以上分析都是抛弃了节点本身信息而言的,一旦节点包含了丰富的可参考信息,这种只考虑边的形式很难加入节点信息进行参考。
因此,结合以上两个问题,图表征学习的目的可以概括为以下两部分:
1)学习一种低维度的向量表示网络节点,将节点映射到相应的向量空间(即|V| \times d,其中d \lll |V|),并能够保持原先的相似度信息。这种网络表征学习就是关于图结构的网络表征学习,也称网络嵌入。
2)我们希望表示不仅仅可以表征网络结构,同时也可以表征节点本身自带的属性,这种表征学习,就是伴随节点属性的网络表征学习。通常第二种表征学习方法都是从第一种方法中推广而来。本文如果不做特别说明,将主要聚焦并默认为第一类网络表征学习,即网络嵌入。
请牢记以上预定义,接下来正式纪录的论文的运行模式和目的将始终围绕以上说明。因此在感到困惑时可以随时回来整理一遍。
最后值得注意的是,表征学习一般需要定义两个函数(往往与学习函数相关),一个是相似度定义,一个是编码器:
Similarity(u,v) \approx Z_u^TZ_v(original space nodes \to embedding space nodes)
ENC(v)=Z_v(v \to mapping \to Z_v)
下面正式开始。
Deepwalk
Deepwalk首次出场于KDD2014,其正式开始了网络嵌入工作的新一轮脉络线,它的主要贡献在于首次将NLP的思想用在网络嵌入上。
因此在讲解Deepwalk之前,需要简单介绍一下本文引入的必要的其它方法:
Deepwalk提到了在学习一个网络表征的时候需要注意的几个性质(自肃环节):
- 适应性:网络表征必须能适应网络的变化。网络是一个动态的图,不断会有新的节点和边添加进来,网络表征需要能适应网络的正常演化而不用重复学习过程。
- 社区性:网络中往往会出现一些特征相似的点构成的团状结构,这些节点表示成向量后必须相似。
- 低维性:数据稀缺时,低维模型会更好。代表每个顶点的向量维数不能过高,过高会有过拟合的风险,对网络中有缺失数据的情况处理能力较差。
- 连续性:低维的向量应该是连续的。
作者发现,在图上进行随机游走,所访问的节点是符合幂律的,即和语言词汇一样,一些词(节点)会被反复使用(访问),整个分布十分相似。这给了作者一种处理思路:是否可以把节点当成单词进行处理,即:
词嵌入是对构成一个句子中的单词序列进行分析,其处理的基本元素是单词。
网络嵌入是对构成一个“序列”中的节点序列进行分析,其处理的基本元素是网络节点。
可以很自然地看出,两种思想是一一对应的,这就是为什么能从NLP中引入这种思想的主要原因。因此,我们需要得到一种网络节点构成的“序列”,这就是随机游走(Random Walks)在此的作用,产生访问节点序列用于词向量模型处理。使用随机游走有以下两个好处:
- 并行化:随机游走是局部的,对于一个大的网络来说,可以同时在不同的顶点开始进行一定长度的随机游走,多个随机游走同时进行,可以减少采样的时间。
- 适应性:可以适应网络局部的变化。网络的演化通常是局部的点和边的变化,这样的变化只会对部分随机游走路径产生影响,因此在网络的演化过程中不需要每一次都重新计算整个网络的随机游走。
在具体实现上,使用固定长度(窗口)的游走序列,这里称为截断随机游走。
讲到这里其实Deepwalk的流程已经大致比较清晰了,其具体步骤分为两大主要部分:首先是随机游走生成游走节点序列(对应算法流程图中的第6行),其次是更新过程,将序列输入模型输出最终Embedding向量(对应算法流程的第7行),流程与算法流程图如下:
算法输入包括图G、模型处理窗口长度w、嵌入向量维度d、每个节点游走数目\gamma以及游走长度t。
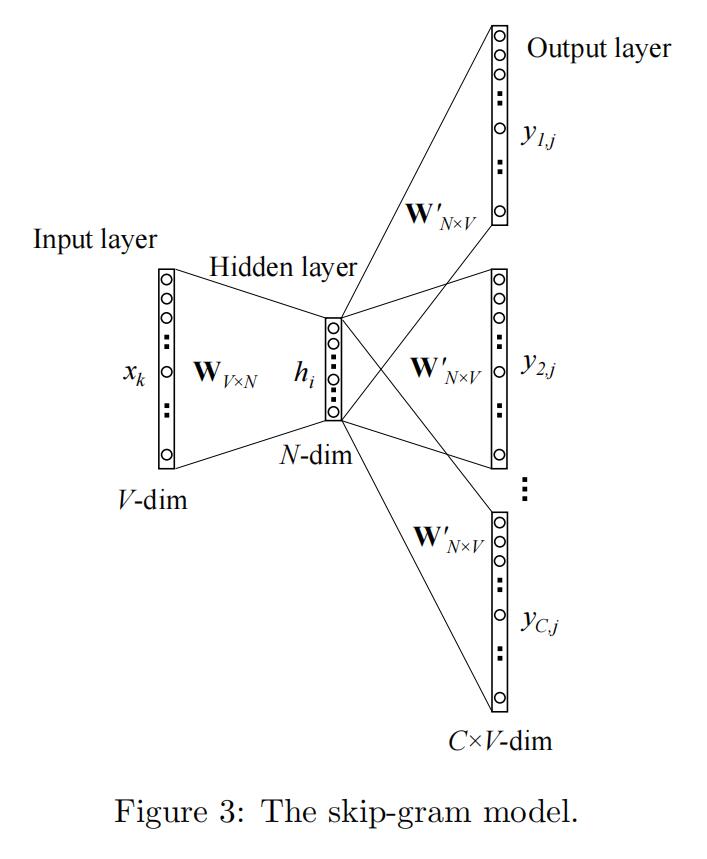
对于Skip-gram,其算法流程图如上。它的目标是使句子中出现在窗口w中的单词的同时出现概率最大化,使用独立假设来近似一个条件概率,如下:
Pr(\{v_{i-w}, ... , v_{i+w}\}\setminus v_i|\phi (v_i))= \prod_{j=i-w, j\neq i}^{i+w}Pr(v_j|\phi (v_i))
而在这一步中,选择分类器(诸如逻辑回归softmax)这类方法在计算时需要访问全部节点(如:S_i=\frac{e_i}{\sum_{j}e_j}),会造成非常恐怖的计算量,因此有两种优化方式。
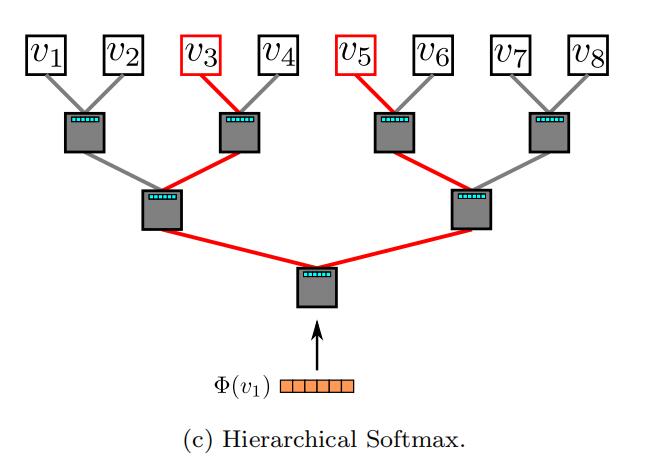
1)hierarchical Softmax
直观来说hierarchical Softmax的思路就是减少计算路径,用Huffman树来存储高频词,通过计算从根节点访问相应叶子节点的路径从而得到条件概率,时间复杂度从O(V)降至O(log_{2}V),Deepwalk采用了该优化方案。
2)negative sampling
负采样的思路则是通过减少计算样本量从而减少计算量。其基本思想是:对于整个词袋,和某个词一起出现的词的个数是很少的,那么不需要区分整个词袋,只要能把正例即希望预测出的词从另外少数随机选择的negative samples 分出来就行了。原理是用下列公式近似:
log(\frac{exp(z_u^Tz_v)}{\sum_{n \in V}exp(z_u^Tz_n)}) \approx log(exp(z_u^Tz_v))- \sum_{i=1}^n log(exp(z_u^Tz_{n_i}))
这一方法还会在之后的论文中被提及。
实验部分
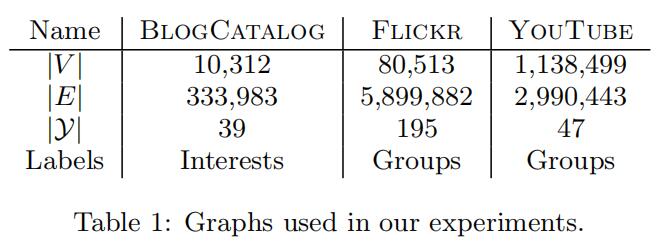
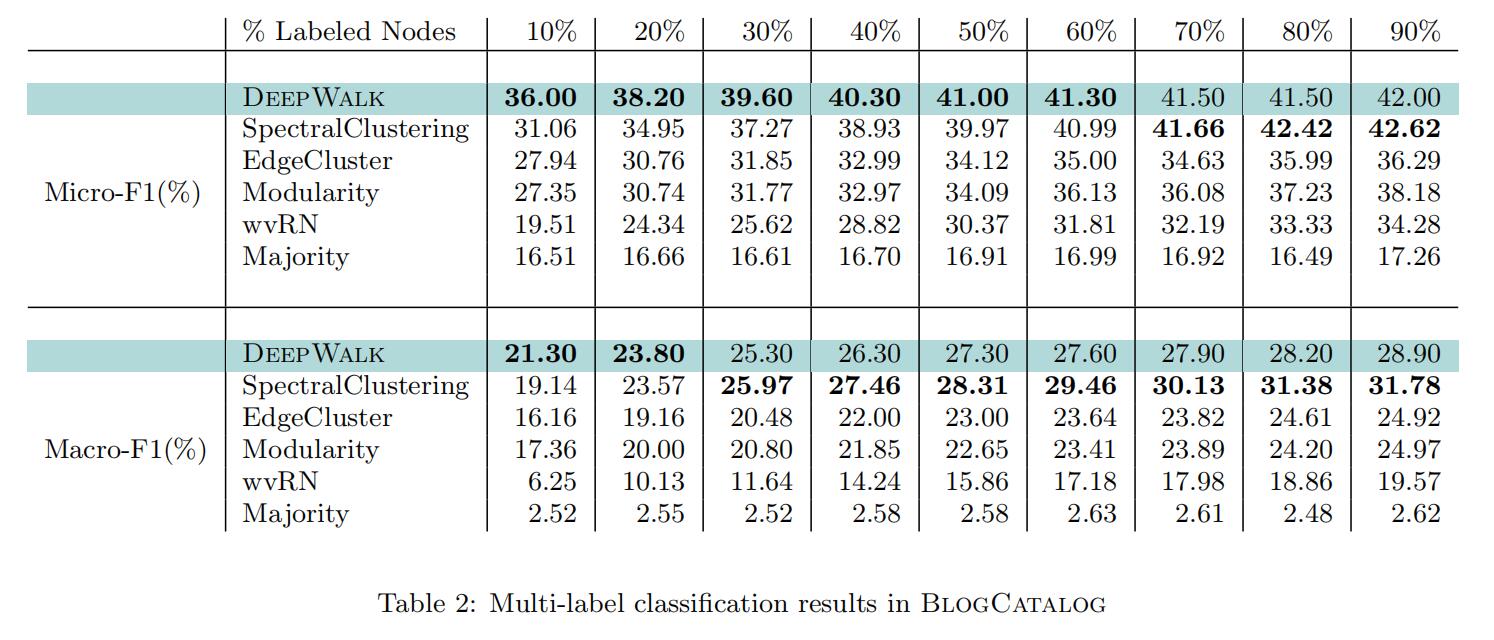
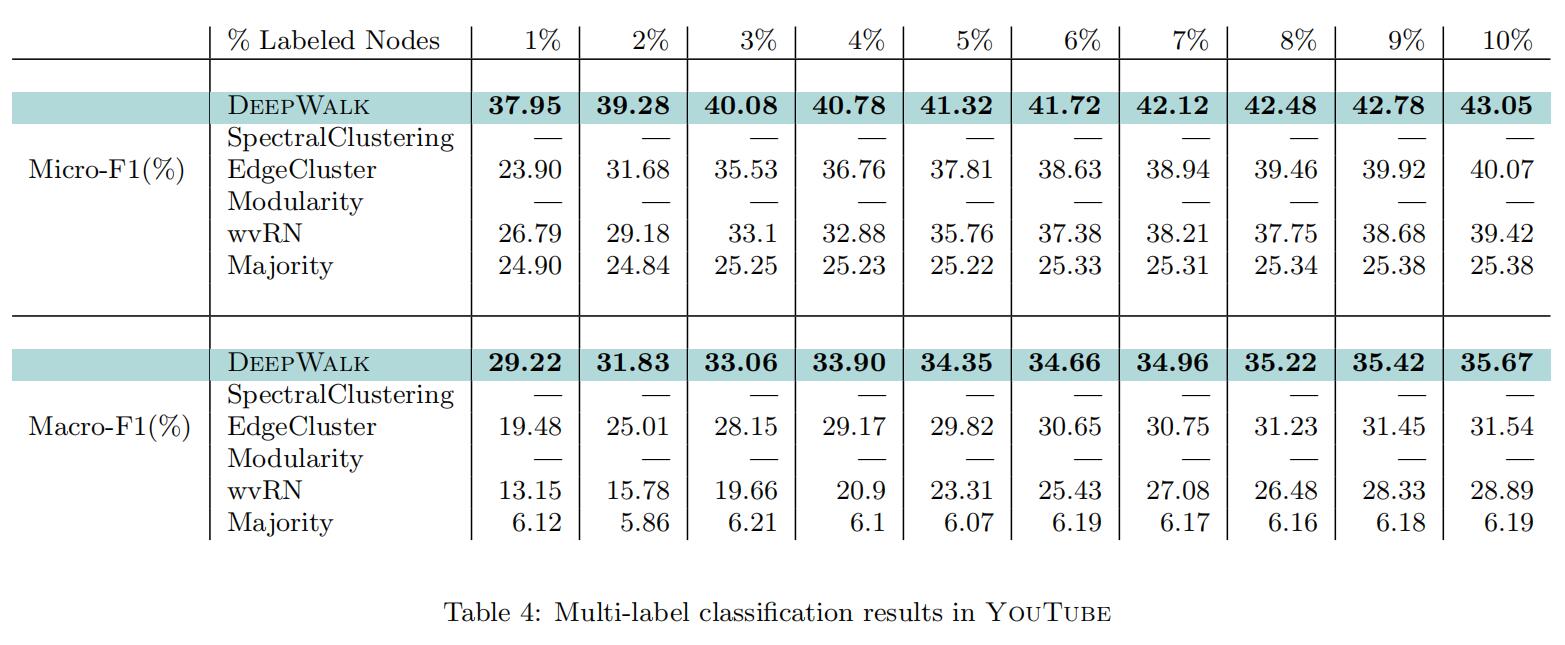
作者在三种社交网络数据集上进行实验:BLOGCATALOG、FLICKR和YOUTUBE(大规模),其具体参数量级如下:
其对比的方法有:SpectralClustering、Modularity、EdgeCluster、wvRN、Majority,均为传统方法。比较指标为Macro-F1和Micro-F1,实验结果如下:
可以看到,Deepwalk的优势之处在于即使只有少量标签样本也可以得出很好的结果,并且在大规模稀疏图上仍然能保持这样的优势。
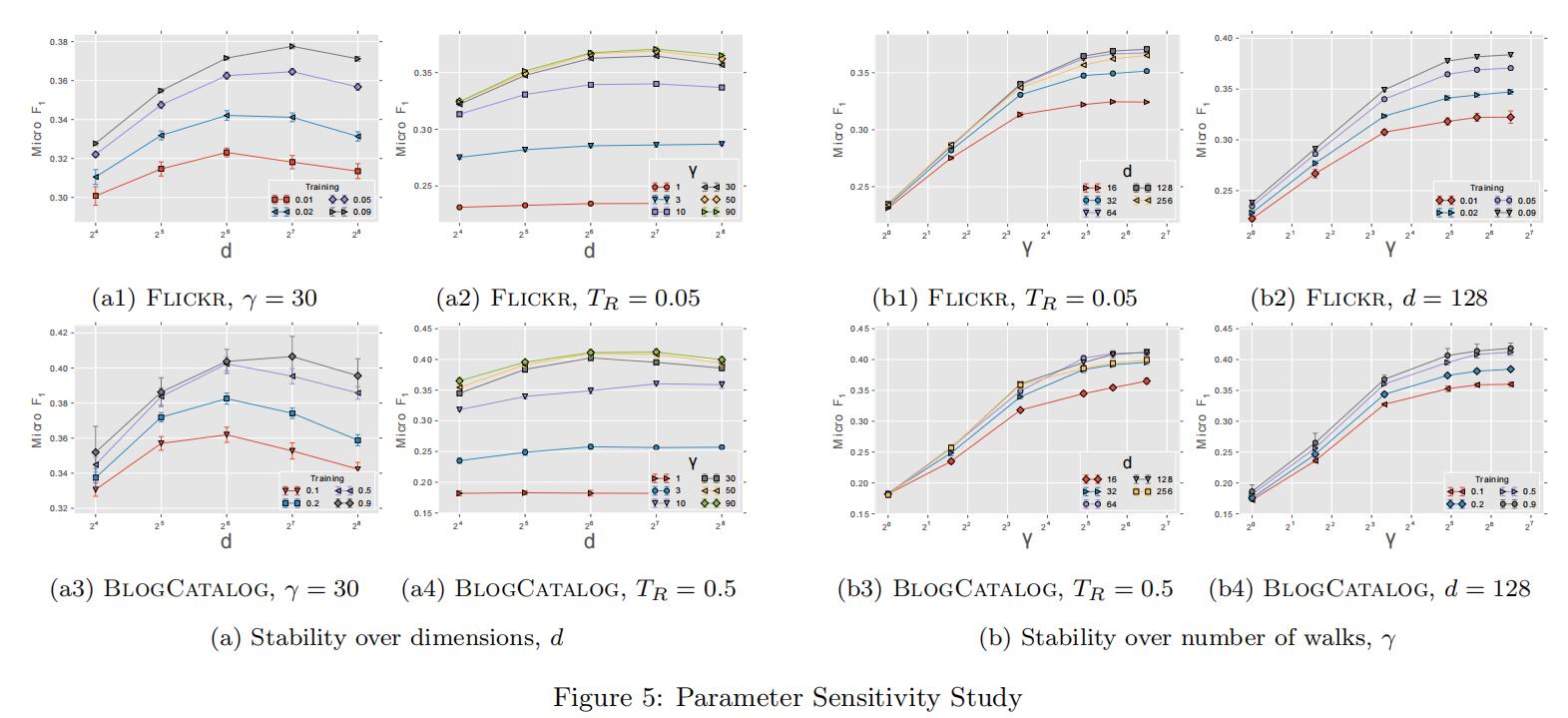
同时,为了评估参数对模型的影响,实验固定了窗口大小和行走的长度,仅改变表征维数、每个顶点行走次数和可用训练量,实验效果如下:
a1和a3表明实验效果受训练示例数目的影响,a2和a4为行走次数找到了合适的值(30)。这些实验表明模型的性能取决于它所看到的随机游动的数量,而模型的适当维数取决于可用的训练示例。图b的实验表明增加行走次数对结果有很大影响,但达到一定峰值后影响很快减慢,这说明只有少量的随机游走是真正有意义的。
本文的核心贡献:
1)做表征学习。
2)提出只用局部信息的可扩展的方法(可在线)。
3)将无监督学习应用在图上。
4)作为将来文章的baseline
当然,这篇文章也不可避免地有它的局限性(随着文章越来越多将被后人反复鞭尸),主要有以下几个方面:在之后我会一一提及
1)只能用于无权图。
2)实验部分已经说明了只有少量随机游走是真正对网络嵌入有意义的,然而Deepwalk并没有提供一种明确目标来表明哪些网络属性要保留下来。






文章评论