（整理）社交网络（一）|不如就从图表征说起

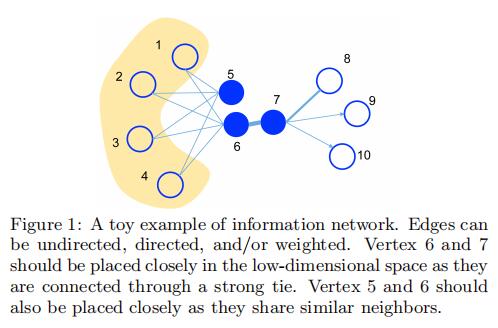
1阶相似度用于描述图中成对节点之间的局部相似度，形式化描述为若u,v之间存在直接连边，则边权w_{uv}即为两个顶点的相似度，若不存在直接连边，则一阶相似度为0。如上图的6和7存在直连边且边权较大，则认为两者相似且1阶相似度很高，而5和6之间不存在直接连边，则两者间1阶相似度为0。

2阶相似度应该是首次由本文提出，我认为是本文主要的贡献点之一。1阶相似度并不足以描述节点间的关联，如上图5和6虽然没有直接连边，但它们有很多相同的邻居节点（1,2,3,4），这也可以说明5和6是相似的，2阶相似度就是用于描述这种关系。形式化定义为，令p_u=(w_{u,1}, ... ,w_{u,|V|})表示顶点u与其他顶点间的一阶相似度，则u和v的2阶相似度可以通过p_u和p_v的相似度表示。若u和v之间不存在相同的邻居节点，则2阶相似度为0。

对于每一条无向边(i, j)，定义顶点v_i和v_j之间的联合概率为：

p_1(v_i,v_j)=\frac{1}{1+exp(-\vec{u_i}^T \cdot \vec{u_j})}

其中\vec{u_i}即为顶点v_i的低维表征向量表示，同时定义经验分布：

\hat{p_1}=\frac{w_{ij}}{W}, W=\sum_{(i,j)\in E}w_{ij}

这样优化目标即为：

O_1=d(\hat{p_1}(. , .), p_1(. , .))

其中d(. , .)用于计算两个分布间的距离，常用的衡量指标有KL散度，忽略掉常数项后，优化目标变为：

O_1=-\sum_{(i,j)\in E}w_{ij}log p_1(v_i, v_j)

需要注意的是这里一阶相似度只适用于无向图。

对于每个节点v_i，维护两个embedding向量，一个是该节点本身的表征向量\vec{u_i}，一个是该节点作为其他顶点的上下文顶点时的表征向量\vec{u_i}'。

同样地，对于每条边(i, j)，定义给定点v_i的情况下，产生上下文邻居节点v_j的概率为：

p_2(v_j|v_i)=\frac{exp(\vec{u_j}'^T \cdot \vec{u_i})}{\sum_{k=1}^{|V|}exp(\vec{u_k}'^T \cdot \vec{u_i})}

其中|V|是节点数或“上下文节点”数目（实际运算结果）。与一阶定义类似，我们有优化目标：

O_2=\sum_{i \in V}\lambda_i d(\hat{p_2}(.|v_i), p_2(.|v_i))

其中\lambda_i为控制节点重要性的因子，可以通过顶点度数、PageRank等方法获得。经验分布定义为：

\hat{p_2}(v_j|v_i)=\frac{w_{ij}}{d_i}

d_i是节点的出度，对于带权图d_i=\sum_{k \in N(i)}w_{ik}。采用KL散度并假设\lambda_i=d_i，忽略常数项，有：

O_2=- \sum_{(i, j)\in E} w_{ij} log p_2(v_j|v_i)

通过学习向量表示\{\vec{u_i}\}和\{\vec{u_i}'\}进行优化，这里有疑问针对\{\vec{u_i}'\}，因为在负采样中实际运算设置为与一阶相同的向量。

可见，二阶相似度适用于有向图和无向图。