（整理）社交网络（一）|不如就从图表征说起

2022年2月15日 967点热度 6人点赞 0条评论

Node2Vec

Node2Vec首次出场于KDD2016，它的主要思路是弥补了之前深度和广度随机游走的不足（~~同时弥补了Deepwalk起名不当的不足~~），并重新从社区的角度进行分析，在代码层面通过biased random walk进行实现。

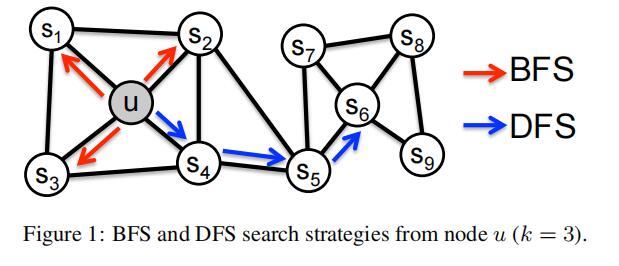
具体来说，在前面两篇文章的介绍下，我们大致可以感受到深度搜索和广度搜索之间需要的一种平衡，本文是这样总结的：通过调整随机游走权重的方法使嵌入结果在网络的同配性（homophily）和结构性（structural equivalence）中进行权衡。同配性指的是距离相近节点的嵌入结果应该尽量相似，如图中节点u与其相连的节点s1、s2、s3、s4的表达应该是接近的，这就是同配性的体现。而结构性指的是结构上相似的节点嵌入结果应该尽量接近，如图中u和节点s6都是各自局域网络的中心节点，结构上相似，其嵌入表达也应该相似，这是结构性的体现。

那么从游走的角度上讲，为了让结果能够表达网络的同配性，游走的过程应该需要更倾向于BFS；另一方面，为了抓住网络的结构性，就需要游走更倾向于DFS。这是很容易不看原文只从图中直观理解的错误看法。事实上，BFS反映了结构性，DFS反映了同配性。简单来解释就是重新回到定义，结构性更加倾向关注节点所处的位置，而非节点本身的属性；同配性则相反，更多关注节点之间的相似性。BFS会把低阶邻居的节点都访问一遍，也就是访问于同一社区内；而DFS可以跳出社区，更快地访问到边缘的节点。试想一下，如果对于两个结构性相近的节点，如果采用BFS，则它们在游走后的序列上下文类似的概率更高，这说明它们在结构上十分类似；而对于两个距离比较近的节点，DFS构建时它们出现相同序列的概率更高，也就更容易学习出相似的嵌入向量。因此，实际上是BFS体现了结构性，DFS体现了同配性。

基于上述所讲，因此本文的优化函数如下，定义与前文类似，十分好理解：

$max_f \sum_{u \in V}log Pr(N_S(u)| f(u))$

这需要基于两个假设：其一是条件独立性假设，即采样每个邻居是相互独立的，即 $Pr(N_S(u)| f(u))=\prod_{n_i \in N_s(u)}Pr(n_i|f(u))$ 。其二是假设特征空间的对称性，即映射后的影响是相互的，一个顶点作为源顶点和作为近邻顶点的时候共享同一套嵌入向量，因此满足： $Pr(n_i|f(u))=\frac{exp(f(n_i)\cdot f(u))}{\sum_{v \in V}exp(f(v) \cdot f(u))}$ 。整合上述3步公式，因此最终的目标函数可以表示为：

$max_f \sum_{u \in V}[-log Z_u+\sum_{n_i \in N_s(u)} f(n_i)\cdot f(u)]$

$Z_u= \sum_{n_i \in N_s(u)} exp(f(n_i)\cdot f(u))$ 为归一化因子，优化方法同之前的负采样方法。

下面介绍核心的有偏的随机游走。

biased random walk

给定一个节点v，访问下一个节点x的概率为：

$P(c_i=x | c_{i-1}=v)=\left\{\begin{matrix}\frac{\pi_{vx}}{Z} & if(v,x)\in E\\0 & \text{otherwise}\\\end{matrix}\right.$

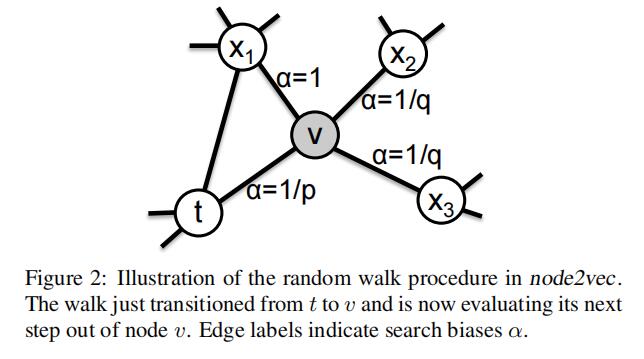
$\pi_{vx}$ 是顶点v和顶点x之间的未归一化转移概率。Node2Vec引入两个超参数p、q来控制随机游走的策略，假设当前随机游走经过边(t,v)到达顶点v，设 $\pi_{vx}=\alpha_{pq}(t,x)\cdot w_{vx}$ ， $w_{vx}$ 是点v、x之间的边权，其中：

$\alpha_{pq}(t,x)=\left\{\begin{matrix}\frac{1}{p} & if d_{tx} = 0\\1 & if d_{tx} = 1\\\frac{1}{q} & if d_{tx} = 2\\\end{matrix}\right.$

$d_{vx}$ 表示顶点t和顶点x之间的最短路径距离。先直观地解释下这个分布：

如果t与x相等，那么采样x的概率为 $\frac{1}{p}$ 。
如果t与x相连，那么采样x的概率为1。
如果t与x不相连，那么采样x的概率为 $\frac{1}{q}$ 。

下面分析超参数p和q对于随机游走的影响。

返回参数p：超参数p只控制重复访问刚刚访问过的节点的概率。注意到p仅作用于 $d_{vx}=0$ 的情况，而这表示x即为v刚访问过的顶点。因此若 $p>max(q,1)$ ，那么采样会尽量不往回走；如果 $p<min(q,1)$ ，那么采样会更倾向于返回上一个节点，这样就会一直在起始点周围某些节点来回访问。

出入参数q：超参数q控制着游走向内还是向外。如果 $q>1$ ，那么游走会倾向于在起始点周围的节点之间跑，可以反映一个节点的BFS特性。如果 $q<1$ ，那么游走会倾向于往远处跑，反映出DFS特性。

当p=q=1时，就等同于DeepWalk里的随机游走。

除了随机游走部分不同外，剩下的步骤和DeepWalk非常类似了。