这一页开始我们的学习需要进入一个缓冲阶段,如同DFS能跳出局限性看到同配性一样,我们需要跳出来看一看基于其它方法的网络嵌入,才能更好的理解当前研究的优越性、局限性以及之后研究的开创性。因此,我打算以综述为大致脉络,为了阅读体验做部分调整。先从基于矩阵分解的方法开始,再回到随机游走方法,然后进行对嵌入方法的一个小结,之后再进入新的方法。矩阵分解这边值得阅读的有GF、GraRep和HOPE。目前出于时间原因选择了GraRep做讲解,后续可能会补上HOPE。
3.28更新:HOPE是一种做有向图上的网络嵌入工作,其本质还是涉及SVD的矩阵分解。由于原文自带综述属性又有复杂证明,全部看完需要追溯到多年前的工作,因此不做相关方向的话应该是不会补了,有兴趣的可以自行了解(HOPE原文为Asymmetric Transitivity Preserving Graph Embedding)。
GraRep: Learning Graph Representations with Global Structural Information
GraRep首次出场于CIKM 2015。与前面方法不同的是,它采用了矩阵分解的方法解决网络嵌入问题。这篇文章提出来时DeepWalk和LINE正流行起来。然而DeepWalk这种直接基于skip-gram的算法,在训练时无法区别出一个节点的邻居的阶数:每个节点在学习自己的表示时,只能知道自己周围k阶邻域中包含哪些节点,而不知道这些节点具体是自己的几阶邻居,表现在优化函数不确切。尽管LINE能够直接区分一阶和二阶邻居,但它无法容易的扩展到捕捉任意k阶邻居的信息上。其中一部分原因是skip-gram实际上将节点之间的各阶关系投影到一个平凡子空间(common subspace)中。因此,本文采用矩阵分解的思路,分别学习网络节点的k阶关系表示,然后将这些表示结合起来作为最终的表示结果,并可以作用于加权图中。
定义图G=(V,E),度矩阵D和邻接矩阵S,于是可以得到一阶转移矩阵:A=D^{-1}S,其中A_{i,j}可以认为是节点i经过一步转移到节点j的概率。同时,讨论到全局特征,包含两方面:一个是即使节点距离很远关系也要被考虑到,即全局信息。另一个是不同阶的关系也要被考虑到。为了说明这一点,用以下图来举例:
图中蓝色节点表示相似的节点,连线的粗细表示关系的强弱。最简单的1阶如a、e所示。然后是b、f,可以看到对于2阶信息来说它们共享的邻居越多,关系就越强。对于3阶,如g图,尽管A1和B之间关系很强,但B、C之间的关系较弱,导致A1与A2关系并不强,而c图由于B和A2之间有大量共享邻居,这些邻居加强了A1和A2之间的关系。类似的,4步信息对于揭示图的全局信息也可能是至关重要的。因此,考虑全局信息是十分重要的。
同样的,考虑不同阶段的信息也是十分重要的,如上图简单的示例。A点受到的信息除了来自B点的一阶信息,还有来自全部C点的二阶信息。如果不区分这些信息的话,可以作出如b图的替代图,其中收到的信息完全相同,但却是完全不同的结构。
因此,所设计的模型需要能够尽可能学习到全局的信息,并集成k阶不同的信息。
我们假设p_k(c|w)表示精确到第k步节点w到节点c的概率,由之前A的定义,我们可以引入k步概率跃迁矩阵A^k=\prod^kA来表示第k阶的转移概率矩阵,这样,有:p_k(c|w)=A_{w,c}^k。然后我们的优化目标就很明确了:1)最大化这个组合所代表的路径在图中的概率。2)最小化除了这个组合外在图中的概率。简单来说,设计了如下的目标函数:
L_k(w)=(\sum_{c\in V}p_k(c|w)log \sigma(\vec{w} \cdot \vec{c}))+\lambda E_{c' \thicksim p_k(V)}[log \sigma(-\vec{w} \cdot \vec{c'})]
\lambda是负采样系数,c'是根据分布采样得到的负样本,这里采用了负采样进行优化,因此,最终的损失函数表达如下:
L_k(w,c)=p_k(c|w)\cdot log \sigma (\vec{w}\cdot \vec{c})+\lambda \cdot p_k(c) \cdot log \sigma (- \vec{w} \cdot \vec{c})
文中提到一个现象:随着k的增长,转移概率会收敛到一个固定值:p_k(c)=\sum_{w'}q(w')p_k(c|w')=\frac{1}{N}\sum_{w'}A_{w',c}^k。其中q'(w)指的是第一次的1/N,全部代入之前的公式,有:
L_k(w,c)=A_{w,c}^k \cdot log \sigma (\vec{w}\cdot \vec{c})+\frac{\lambda}{N} \cdot \sum_{w'}A_{w',c}^k \cdot log \sigma (- \vec{w} \cdot \vec{c})
对该式求极值,得到这样一组关系:\vec{w} \cdot \vec{c}= log(\frac{A_{w,c}^k}{\sum_{w'}A_{w',c}^k})-log(\beta),其中\beta=\lambda/N。到这一步就可以解释许多之前的工作了:我们要做的无非就是找到这样一个矩阵Y,它编码了网络中所有节点相互之间的关系,但是这个矩阵维数很高(|V|x|V|),不能直接用来做网络表示。因此用矩阵分解的方法对Y进行分解,分解后的W、C原小于Y的维度。其中W矩阵就是网络节点的表示,C矩阵就是上下文节点的表示(我们不关心这个矩阵):
Y_{i,j}^k=W_i^k \cdot C_j^k =log(\frac{A_{i,j}^k}{\sum_t A_{t,j}^k})-log(\beta)
现在我们已经证明了优化所提出的损失本质上涉及到一个矩阵分解问题。接下来的目标就比较明确了。首先为了降低误差,替换Y中全部负值为0,形成新的矩阵X:X_{i,j}^k=max(Y_{i,j}^k,0)。然后用SVD分解,由于最终要求嵌入至d维,这里直接一步到位:X^k \approx X_d^k=U_d^k\sum_d^k (V_d^k)^T。参考我们的目标,自然的想到:W^k=U_d^k(\sum_d^k)^{1/2}、C^k=(\sum_d^k)^{1/2}(V_d^k)^T,这样就完成了全部的算法目标。
最后的算法流程分为3步:
- 获得k阶转移矩阵。
- 获得k阶节点表示。
- 连接所有表示。
文章接着做了比较类Skip-Gram模型以及采样和转移概率之间关系的研究,这一部分讲解的很少,我的理解可能会有偏差,请辨证地看待,以原文描述为主。
作者首先自行搭建了一个特别的Enhanced SGNS(Skip-Gram model with Negative sampling)。然后设定总的损失即为L=f(L_1,L_2,...,L_K),f为线性求和函数。关注一个特定节点对(w,c),类似上述的分析求导,有Y_{i,j}^{E-SGNS}=log(\frac{M_{i,j}}{\sum_tM_{t,j}})-log(\beta),其中M=A^1+A^2+...+A^K。这里E-SGNS与GraRep的不同在于总loss为线性组合,即每个损失有相同的权重(这是一个很强的假设)。
然后,作者阐明了转移矩阵和采样之间的关系。在随机游走生成的序列中,假设顶点w总共出现\#(w)=\gamma \cdot K次,那么对应的1阶邻居c1出现的次数为\#(w,c_1)=\gamma \cdot K \cdot p_1(c|w),对应的2阶邻居出现次数为\#(w,c_2)=\gamma \cdot K \sum_{c'}p(c_2|c')\cdot p(c'|w)=\gamma \cdot K \cdot p_2(c|w),以此类推并把结果相加,可得:\#(w,c)=\gamma \cdot \sum_{k=1}^K p_k(c|w)。由上一段对矩阵的定义,有\#(w,c)=\gamma \cdot M_{w,c}。
现在我们可以计算以c为上下文顶点的预期次数\#(c)=\gamma \cdot \sum_tM_{t,c}。然后把这些表达式全部代入E-SGNS中,有Y_{w,c}^{E-SGNS}=log(\frac{\#(w,c)\cdot |D|}{\#(w) \cdot \#(c)})-log(\lambda)。其中D指的是序列中所有观察到的配对的集合,|D|=\gamma KN。这样转换后的矩阵就和矩阵分解里的形式完全一致。
因此作者得出结论认为SGNS本质上是GraRep的一个用采样方式处理的特例。(这里需要去参阅一篇引用的NIPS2014的原文,该原文也是讨论SGNS与PMI的一致性,与本步骤思想类似。而后来也有文章认为这部分推论不成立,原因在于等价的前提是w、c可取无限长,也就是无限个参数可用。然而这样一来该等价性问题又可以被视为是一种回归问题,那么得到这种等价结果也是合理的,因此在开头提到这一部分需要辨证地看待,后续有缘的话可能会继续跟进)
实验部分
为了展示GraRep的性能,在三种不同的数据集上进行实验 ——社交网络,语言网络和引文网络,包括加权图和非加权图,任务包括聚类、分类和可视化。
数据集分为20-Newsgroup(完全连通加权图)、Blogcatalog(社交网络无权图)、DBLP(引文网络),具体参数见后图。比较的方法为:LINE、DeepWalk、E-SGNS、谱聚类。评价指标为NMI和召回率。
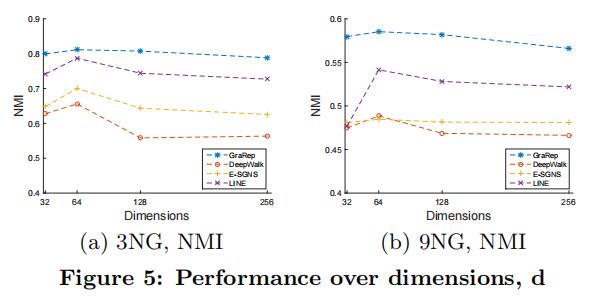
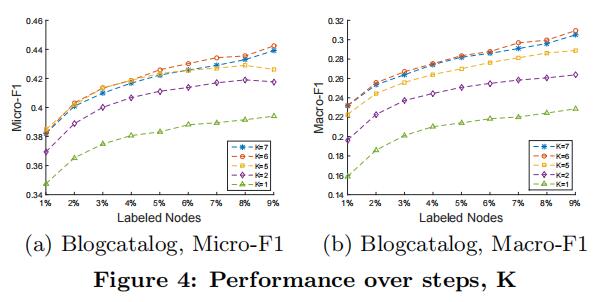
结果如图。对于图3,部分更加细致的结果由于效果更差所以作者没有挂出,可以看到GraRep在小图上和LINE一样可以获得很好的结果。对于维度,作者提到更多的维度并不能提供更多的补充信息,这一点在DeepWalk的实验中参数研究里也有说明。图4表明GraRep学习到不同类型的丰富局部信息用于互相补充,以获取全局结构属性,特别是当数据稀疏时。图5的聚类效果中可以更好的把分界线划分出来,KL散度数据也说明了这一点。
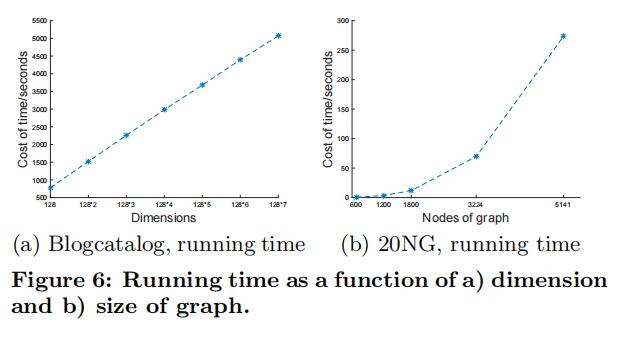
参数敏感性研究,首先是k值的影响,实验在k=4之前都保持上升趋势,说明了k值越高能学到越多信息,而再往后的增加并不能获得更好的效果。维度实验,主要作为表3的补充实验,目前在64维可以获得最佳效果。运行时间实验,随k值增加呈现线性增长,而b图实验随图形大小增加运行时间显著增加,导致时间大幅增加的原因主要是矩阵计算和SVD组件部分。
总结一下,本文从矩阵分解的角度出发,很好地从矩阵角度解释了网络嵌入的原理,并运用了k阶信息,取得了不错的实验效果。并且结合了和Skip-Gram系的比较和区分,从某一方面也体现了科研的多样性。当然,矩阵分解带来的昂贵的计算代价也是难以避免的。这将在不久的将来,为引入深度体系架构埋下伏笔。
HARP: Hierarchical Representation Learning for Networks
接下来的几篇网络嵌入相关的文章,或许没有前面的3篇影响力那么大,但是其思想在整个“前嵌入”阶段是很值得学习的。就好比对于 “word2vec的参数解读”这样的文章自然是不如原文那样影响巨大,但不能说其是没有意义的,对于了解这一技术领域和科普起到了重要的作用。如果说那几篇着墨较多的文章是主菜的话,那这几篇文章就是点缀的开胃小菜。这篇文章也是如此,能在几年后被收录至综述中被提及已经证明了其价值,这里主要去理解其思路为主。
HARP出场于AAAI2018(当年的AAAI)。这篇文章所解决的问题是DeepWalk、LINE、Node2Vec的通病:1)由于采样的原因,会局限于单个节点周围的结构,甚至是低阶邻居,因此会忽略高阶信息。2)本质上是处理非凸优化问题,会陷入局部最优。为了解决这一问题,本文提出了一种元策略,即先将图进行坍缩简化,简化后的图节点对会少很多,图直径下降因此更容易获得全局信息。然后再运行这些网络嵌入算法。
文章比较简单,这里直接放算法流程图:
算法主要分为4步:
- 图粗粒度化(对应算法第1行),依次创建较小的图结构。
- 在最粗化图上运行嵌入算法(对应算法2-3行)。
- 嵌入表示的延长和改善(对应算法4-7行)。
- 获得整个原图的网络嵌入表示(算法第8行)。
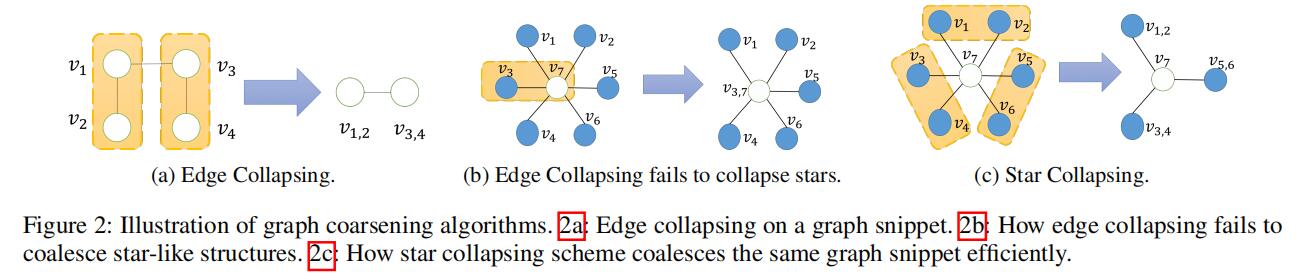
关于图粗粒化算法,涉及到边坍缩算法,有兴趣的可以自行查阅。这里对原文的算法做简单的介绍。简单来说边坍缩的思路是避免两条边指向同一个节点,因此对于a图简单的情况,直接删去其中一条边并合并(合并顺序不影响)。然而对于星形结构,仅仅删去一条边还不够(如b图),因此需要将相邻的点合并删除(如c图)。因此最终算法思路是先进行星形坍缩再进行边坍缩。而由于我们有每个阶段的图,其中的节点要么是保留的要么是新生成的,因此可以简单的利用嵌入结果去还原原图。
实验部分
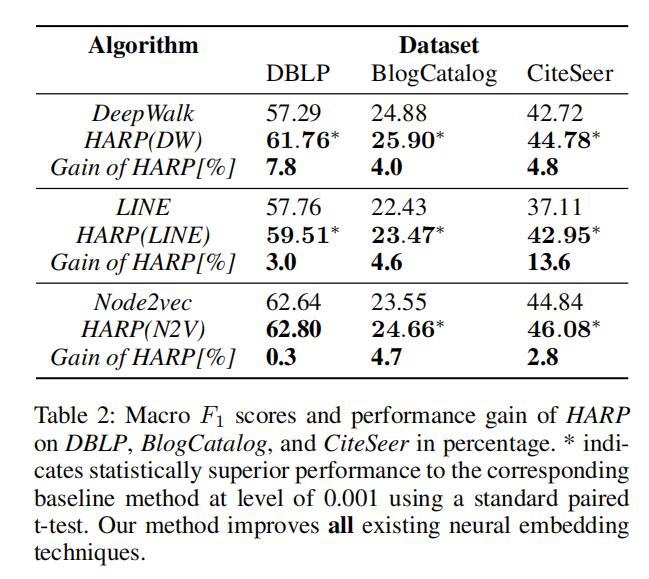
实验采用的数据集为DBLP、BlogCatalog和CiteSeer。比较算法为原3种算法与加入Harp的3种算法,评价标准为召回率。数据集和实验结果如下: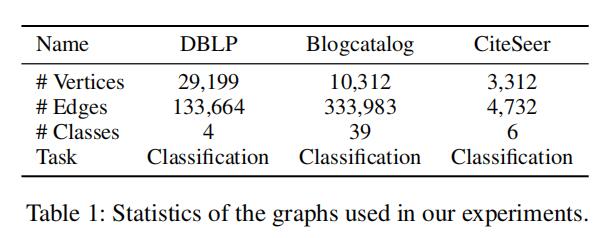
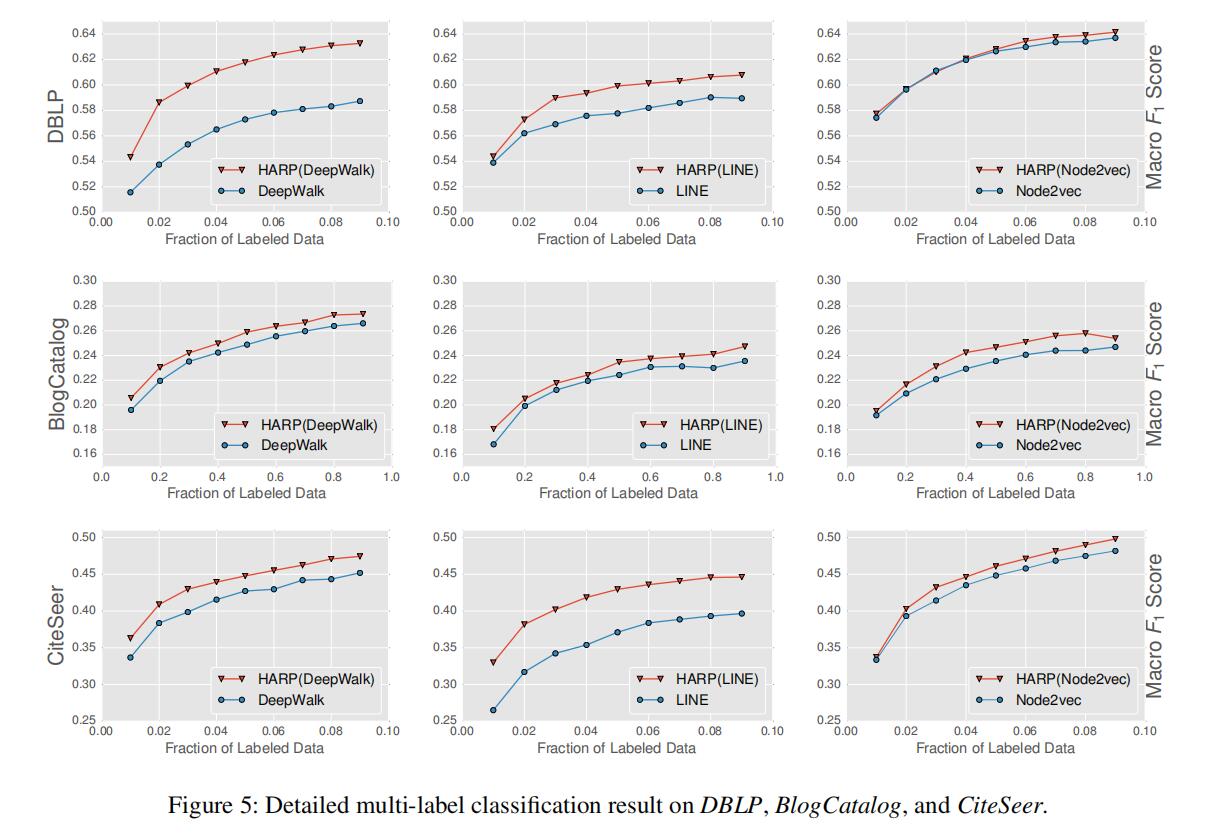
为了公平实验保证了基本参数和采样数据量一致。最终结果如图4,Harp方法均有较大提升。调整标签数据量,加入Harp方法后始终可以获得更多全局信息。尽管部分数据集上存在大量星状结构,图粗化难度较大,Harp仍然可以获取更多的全局信息。(考虑到出版年份,Harp确实是不错的思路,此外笔者感觉实验又又又体现了Node2Vec可以挖掘高阶信息)。
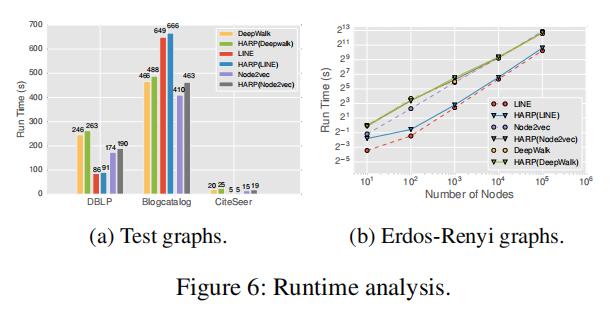
最后是运行时间比较,可以看到简化图和还原图的操作并没有带来大量的时间消耗,本质上还是嵌入操作占主要部分。
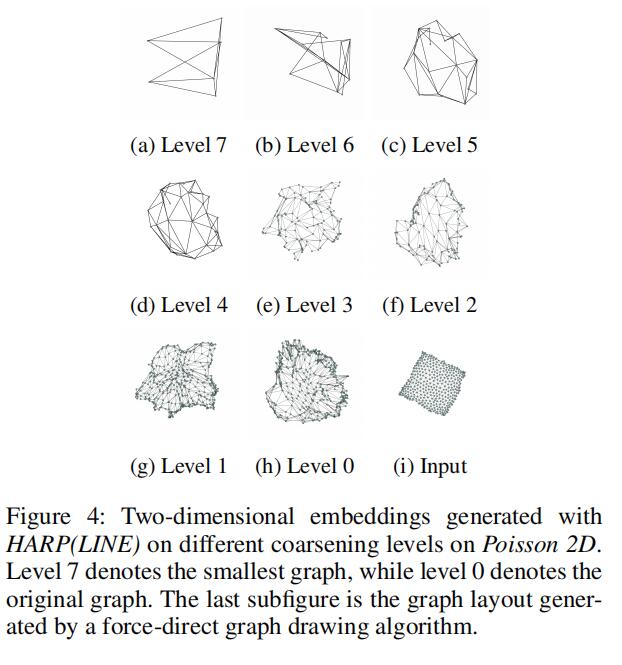
展示一下简化图的结构比较,个人认为这部分更能直观体现Harp的特点:
个人感想,这篇文章“避其锋芒”但又尝试解决了本质性的问题,其采用边坍缩的思想事实上在后来推荐系统一些文章上也有类似的操作,采用卷积等聚合操作,不过都是后话。总之其思想还是很有意思的。
Walklets: Multiscale Graph Embeddings for Interpretable Network Classification
本文改名后发表于ASONAM 2017,作者是DeepWalk原作者,总结了最近的工作(LINE、GraRep)后对原先DeepWalk做出改进。DeepWalk的缺陷之前也提到过:不能获取高阶信息、由于基于采样多阶信息被强行拉至同一平面、只能用于无权图。由于上面讲解了GraRep,所以这篇文章的理解将非常简单:因为k阶的矩阵保存了所有k长度的路径,因此简单来说,就是用采样的方法去拟合矩阵中的这些路径。
作者先分析了DeepWalk和LINE本质上和矩阵分解之间的联系(原文这部分很略写,最终表达和GraRep里表达的思想十分类似),并证明了由于路径数量导致采样时高阶路径不一定会被采样到。然后在采样的具体操作上,跳过一些节点总而生成各个长度的所有路径,如下图,非常容易理解:
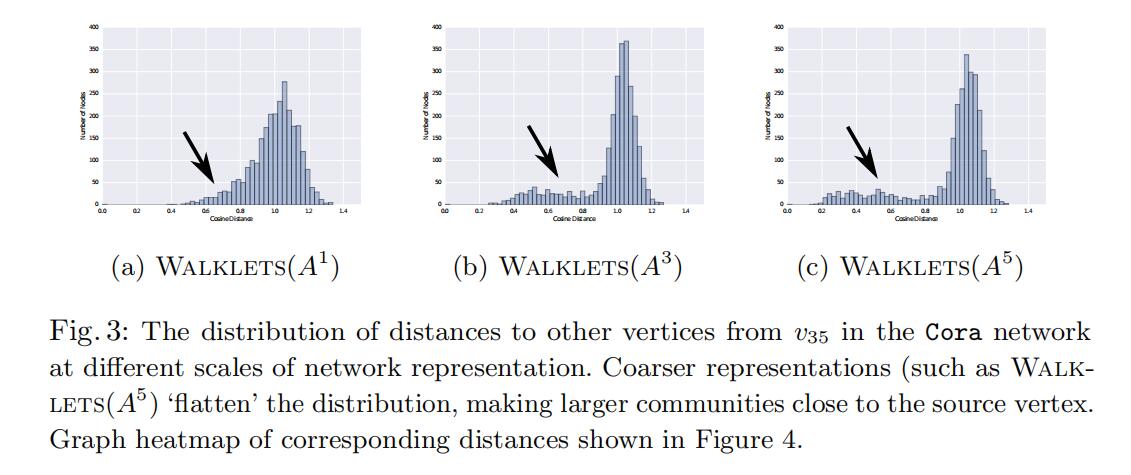
这样的采样方式直观上可以扁平化距离分布,使得更高阶的信息可以被采样到(Cora上测试):
很明显这样可以采集到k阶矩阵的所有路径,从而达到采样方法和矩阵分解之间的等价性。同时,采样的方法所需的计算资源更少。我们直接上实验分析。
实验部分
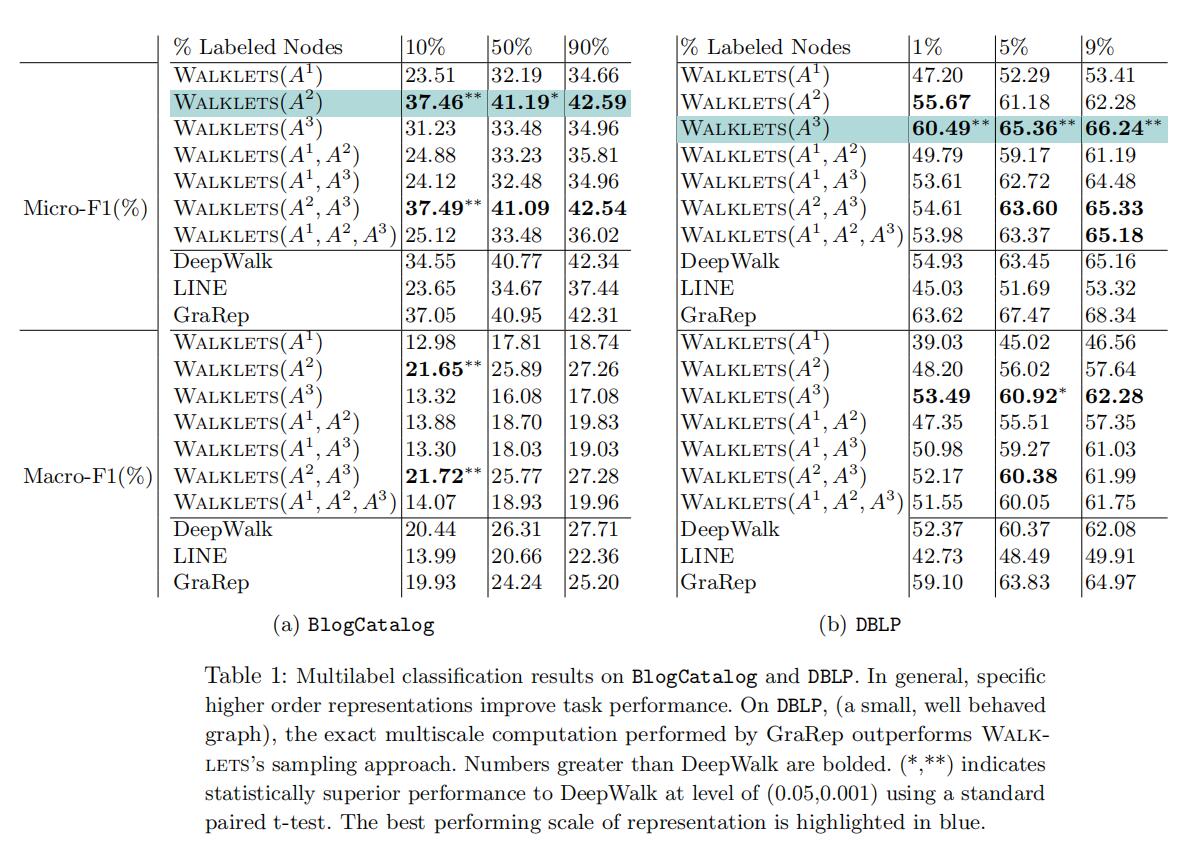
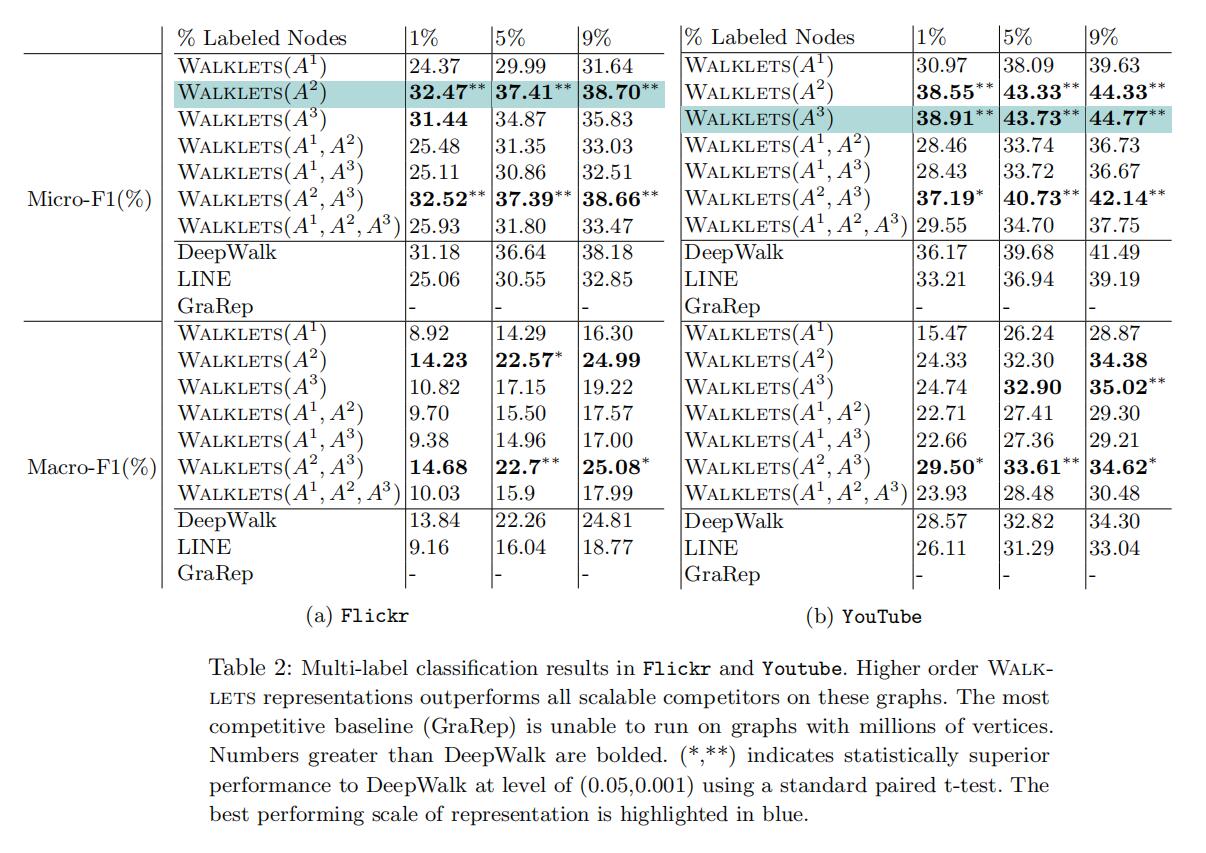
实验数据集分为BlogCatalog、DBLP、Flickr、YouTube,比较方法毫无疑问:DeepWalk、LINE、GraRep(重点比较对象),评估指标为召回率。
实验结果值得关注的点在于:Walklets没有任何一个单一尺度的方法可以全部图通吃,说明了部分图是存在分层信息以及获取多尺度信息的必要性,这些信息可以补充缺少的信息。Walklets在所有数据集上都取得了不错的表现,DBLP上GraRep表现更好是因为网络全连接时直接矩阵计算会获取更多信息。而图一旦增大(后两个数据集)GraRep计算量剧增无法运行,这证明了Walklets在大型图上的能力。同时Walklets(2)的高性能可以使得更好获得新加入的节点,这也是Walklets作为在线算法的一大优势。






文章评论