（整理）社交网络（一）|不如就从图表征说起

前面的小结中总结了浅层嵌入这种类编码器结构的3种缺点，这种观点被后人广泛认可。在正式介绍图神经网络之前，我们将继续沿着嵌入工作的路线走，介绍两篇用其他方法且影响力较大的网络嵌入相关文章，看看它们是从什么角度解决、怎么解决这3个问题的。

Structural Deep Network Embedding

简称SDNE，首次登场于KDD2016。它主要解决的是3种问题中的第一种，并且主要修改对象为LINE，采用了自编码器的模型结构，是早期将神经网络运用在网络表示工作上的文章。

SDNE可以看作是LINE的拓展，其思路是使用一个自编码器结构来同时优化1阶和2阶相似度（LINE是分别优化的），学习得到的向量表示能够保留局部和全局结构，并且对稀疏网络具有鲁棒性。

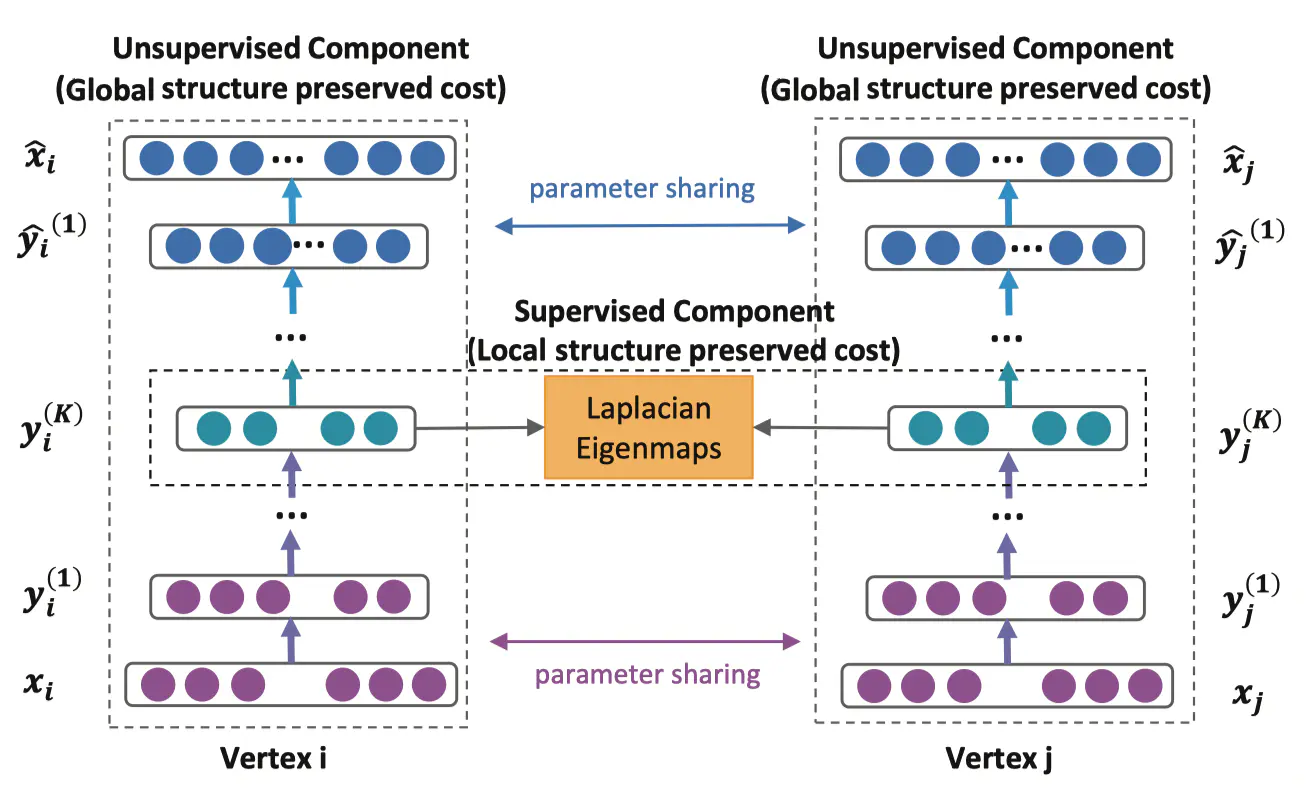
SDNE的主体框架如下：（原文图局部和全局画反了，这里给出修正后的版本）

先看左边，是一个自编码器的结构，输入输出分别是邻接矩阵和重构后的邻接矩阵。通过优化重构损失可以保留顶点的全局结构特征（即获得二阶信息）。再看中间一排，y_i^{(K)}是我们需要的embedding向量，模型通过1阶损失函数使得邻接的顶点对应的embedding向量接近，从而保留顶点的局部结构特征。

SDNE中涉及的符号参数如下：

SDNE的相似度定义与LINE是一样的，因此介绍其优化目标也将轻松许多。

2阶相似度优化目标为：L_{2nd}=\sum_{i=1}^n||\hat{x_i}-x_i||_2^2

对于2阶相似度优化目标，使用图的邻接矩阵作为输入，对于第i个顶点，有x_i=s_i，每一个s_i都包含了顶点的邻居结构信息，所以这样的重构过程能够使得结构相似的顶点具有相似的embedding表示。此外，由于图的稀疏性，矩阵中非0元素是远小于0元素的，那么对于神经网络来说全输出0也会取得不错的结果，然而这并不是我们想要的。

文中给出的解决方法为使用带权的损失函数，对于非0元素具有更高的惩罚系数。修正后的损失函数为：

其中\odot为Hadamard积，b_i=\{b_{i,j}\}_{j=1}^n，若s_{i,j}=0，则b_{i,j}=1，否则b_{i,j}=\beta >1。

1阶相似度的优化目标为：L_{1st}=\sum_{i,j=1}^n s_{i,j}||y_i^(K)-y_j^(K)||_2^2=\sum_{i,j=1}^n s_{i,j}||y_i-y_j||_2^2

该损失函数可以让图中两个相邻的顶点对应的embedding在隐藏空间相近。

整体优化目标：

L_{reg}是正则化项，\alpha为控制1阶损失的参数，v为控制正则化的参数。