（整理）社交网络（一）|不如就从图表征说起

struc2vec: Learning Node Representations from Structural Identity

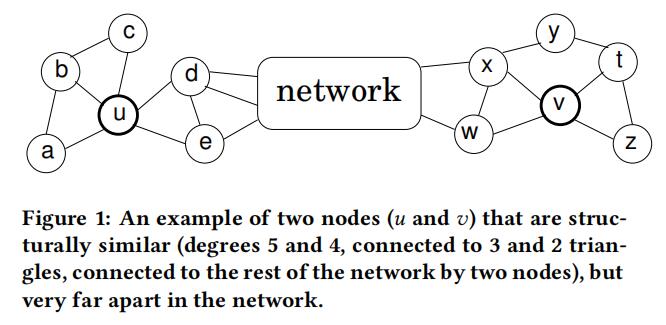
Struc2vec首次登场于KDD 2017，它和之前的文章都不太一样（文风也晦涩难懂，写得和散文一样……），它所关注的是Node2vec中的结构等价性。之前的很多网络表示的工作的思路是利用邻居作为上下文。如果两个节点的共同邻居越多，那么表示这两个节点越相似，自然就要减小他们在嵌入空间中的距离。但是这种方法无法鉴别结构相似但是距离非常远的节点对，换句话说某些节点有着类似的拓扑结构，但是它们离得太远，不可能有共同邻居（就比如下图的u和v）。这种情况是之前很多工作没有考虑到的点。

DeepWalk或node2vec这一类的方法在判断节点的结构是否等价的分类任务上往往并不能取得好的效果。其根本原因在于网络中的节点具有同配性（homohily），即两个节点有边相连是因为它们有着某种十分相似的特征。因此在网络中相距比较近的节点在嵌入空间也比较近，因为他们有着共同的特征；而在网络中相距比较远的节点，则认为它们没有共同特征，因此在嵌入空间的距离也会比较远，尽管两个节点可能在局部的拓扑结构上是相似的。

如果分类任务更看重同配性的特征，那么DeepWalk类的方法自然可以满足要求；但是术业有专攻，如果分类任务是想找出哪些节点的局部拓扑结构是相似的，那么DeepWalk自然就不能胜任了。因此，本文的工作主要在于探究节点的结构特性，从而进行网络嵌入。

文章首先提出了，一个好的可以反映节点结构特性的方法必须满足以下两个特征：

1）嵌入空间的距离得能反映出节点之间的结构相似性，两个局部拓扑结构相似的节点在嵌入空间的距离应该相近。

2）节点的结构相似性不依赖于节点或边的属性甚至是节点的标签信息。

总的来说，本文的算法可以分成四步：

1. 根据不同距离的邻居信息分别算出每个节点对的结构相似度，这涉及到了不同层次的结构相似度的计算。
2. 构建一个多层次的带权重网络M，每个层次中的节点皆由原网络中的节点构成。
3. 在M中生成随机游走，为每个节点采样出上下文。
4. 使用word2vec的方法对采样出的随机游走序列学习出每个节点的节点表示。

接下来来具体探究每个步骤。

首先是定义一种度量节点相似度的方法，按照需要这种方法应该独立于节点和边的属性。作者设计的核心观点是：如果两个节点的度相同，那么这两个节点结构相似；如果这两个节点的邻居度也相同，那么这两个节点的结构相似性比前者更高。

因此，在以往预定义的基础上，作者定义R_k(u)为与节点u距离k的节点集合，例如R_1(u)就是u的直接邻居。s(S)为对某个节点集合V中的节点按照度的从小到大顺序排序后形成的序列。f_k(u,v)为考虑两个节点的k跳邻域时，两个节点的结构距离，具体定义如下：

这是一个递归定义且g(D_1,D_2)表示两个有序序列的距离。可以看到f函数是一个关于k的单调不降的函数，并且只有在两个节点同时存在k跳邻域时才有定义。同时文中用于衡量的g函数为DTW，具体定义为d(a,b)=\frac{max(a,b)}{min(a,b)}-1。

然后介绍作者设计的多层带权重网络M。

每一层是一个带权重的完全图，每条边的权值定义为w_k(u,v)=e^{-f_k(u,v)}, k=0,...,k*

层与层之间用有向边相连，具体的，对于第k层的任意节点u_k，都有有向边(u_k,u_{k-1})和(u_k,u_{k+1})，权重分别为：

其中\tau_k(u)表示第k层中，所有指向u的边中权重大于该层平均权重的数量，具体为：\tau_k(u)=\sum_{v\in V}1(w_k(u,v)>\bar{w_k})。

\bar{w_k}为第k层中，所有指向u的边中权重大于该层平均权重的数量。也就是说，实际上\tau_k(u)表示了第k层中，有多少节点是与节点u相似的，如果很多相似点，说明此时处于低层次，考虑信息少，此时不适合将本层节点作为上下文了，应该考虑跳到更高层去找合适的上下文，所以去更高层的权重更大。

搭建的网络M用于寻找合适的上下文，寻找方法即为DeepWalk里的随机游走。

具体的，假设游走到了u_k，那么下一步可能是u_{k+1},u_{k-1},v_k（本层相连其他点）。留在本层的概率为q，那么跳层的概率为1-q。

在本层中，向其他节点游走的概率跟边的权重有关，也就是对权重做一次归一化得到概率：p_k(u,v)=\frac{e^{-f_k(u,v)}}{Z_k(u)}，分母为归一化因子。

如果跳层，同样分两个方向，也和权重相关：

注意到当层数越高，因为因为考虑的邻域更广，节点间的结构相似性计算越苛刻，因此在底层计算出两个节点结构相似的，在高层则不一定相似，并且高层很多节点之间的f_k(u,v)可能根本没有定义。这就导致如果随机游走在某个节点u跳到了更高的层，那么在随机游走的序列中，其左边的节点是k层，而右边的节点是k+1层的。而左右两边的取值范围是不同的。换言之，某个节点可能会出现在左边，但不会出现在右边，因为虽然它跟中间那个节点u在k层是相似的，但在k+1层可能无定义或者f_k(u,v)太大导致随机游走在k=1层走到这个节点的概率几乎可以忽略。

之后算法只需要直接套用SGNS就行了。

写到这里，笔记总结的第一章——社交网络图表征相关就要告一段落了。总结一下这一章梳理了2014-2017之间的图嵌入工作，现在来看还真是不小的工作量……但是还是非常有意思的，如果全部看完的话可以发现从传统方法到随机游走再到将来的深度学习其实是很自然的。下一次总结应该就是进入现代化的GCN部分了，资料还是挺多的，毕竟有价值的东西太多了，坑还是要慢慢填，慢慢咕咕咕吧 :D