本文是作者在滴滴出行实习时发表的一篇文章，目的是出租车需求预测，特点在于结合了时间、空间、语义三方面的信息，运用多视图深度学习模型。
文章收录于AAAI 2018、
本文内容为个人翻译+创作，如有编写错误之处欢迎指正！
原文地址：立即下载
前言
出租车需求预测是智能城市中智能交通系统的重要组成部分 。一个准确的预测模型可以帮助城市预先分配资源来满足旅行需求并减少空车、浪费资源。
然而，传统的需求预测主要依赖于时间序列预测（Time Series Forecasting），无法模拟复杂的非线性时空关系；现有的预测方法只有独立地考虑空间关系（例如，使用CNN）或时间关系 （例如，使用LSTM）。
因此，我们提出深层多视图时空网络（ Deep Multi-View Spatial-Temporal Network，DMVST-Net）来模拟空间和时间关系。
Specifically, our proposed model consists of three views:
Spatial view (modeling local spatial correlations via local CNN)
Temporal view (modeling correlations between future demand values with near time points via LSTM)
Semantic view (modeling correlations among regions sharing similar temporal patterns)
简单来说，文章中所定义的DMVST-Net 由三部分模型搭建而成：
空间视图（通过本地CNN对本地区的空间相关性进行建模）
时间视图（通过LSTM对未来需求值与近期时间点之间的相关性建模）
语义视图（对共享相似时间的区域之间的相关性建模）
本文贡献
提出一个统一的多视图模型,共同考虑空间，时间和语义关系（spatial, temporal, and semantic relations.）。
提出了一个捕获局部特征与其相关邻近地区的局部CNN模型
基于需求模式的相似性构建了区域图 ，以模拟相关联但空间上遥远的地区。区域之间的潜在语义通过图形嵌入（graph embedding）进行学习。
在滴滴出行提供的大型出租车数据集上进行了大量实验。结果表明我们的方法始终优于已有方法。
DMVST-Net
1.参数定义与预处理
不重叠的区域： L=\{l_0,l_1,…,l_t…, l_T\}
时间间隔，每段30min： I=\{ I_0,I_1,…,I_t…, I_T\}.
出租车情求（Taxi Request）: o (o.t,o.l,o.u)
其中每个变量分别表示时间、位置、用户Id, 用户Id用来过滤重复请求
需求（Demand）:定义为在一个位置i、每个时间点t对出租车的需求量。
y_t^i=|{o:o.t ϵ I_t Λ o.l∈I_i}| 其中|⋅|表示集合
需求预测问题（Demand Prediction Problem）：已知到t时刻的数据，预测t+1时刻的需求量、
y^i_{1+t}=F(y_{t-h,…,t}^L , ε_{t-h,…,t}^L)其中y_{t-h,…,t}^L 表示历史需求 , ε_{t-h,…,t}^L) 表示位置在时间段t-h至t的上下文特征
F()为预测函数
e_{t}^i 表示位置i在特征时间t的特征向量（之后会用到），r是特征个数。
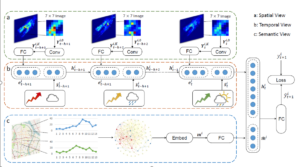
2.整体框架
很重要的一张图，接下来会一一介绍
注明：论文中b部分有几处笔误。首先e和s的对应关系反了，其次第二处s对应的下标时间写错了。
空间视角：局部CNN
首先说明：图像范围太大的话，包含了弱相关区域，会有负效果；根据地理学第一定律，只取邻近区域作为空间表示
“At each time interval t, we treat one location i with its surrounding neighborhood as one S x S image”
取S*S大小图像表示空间特征，则维度为S*S*1，卷积过程为 ：
Y_t^{i,k}=f(Y_t^{i,k-1}∗W_t^k+b_t^k)
其中Y_t^i∈R^{S×S×1}
并为激活函数添加约束：f(z)=max(0,z)
经过k层卷积之后，传递给展平层再全连接降维得到空间表示：
\hat s _t^i=f(w_t^{fc}s_t^i+b_t^{fc})
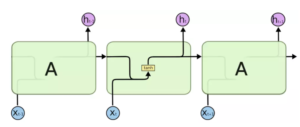
时间视角：LSTM
时间视角采用原始的LSTM模型，非常适合解决时序相关问题。
这里给出LSTM相关模型参考。非原文所含图解。
原文给出所用参数：
其中“º”运算表示Hadamard product，并且定义g_t^i=\hat s_t^i⊕e_t^i，其中⊕为连接运算符
这一部分原图有两处笔误，已在上文说明。
语义视角：结构嵌入
核心：相似的区域不一定相邻 （例如工作日早晨居民区与双休日商业区）
定义一个位置图结构G=(V,E,D)，每个位置作为结点，结点之间两两成边全连接，D是相似性，V=L E∈V×V , D由DTW加衰减计算得到，公式：
ω_{ij}=exp(-αDTW(i,j))
其中α为控制距离衰减率的参数，本文中设为1。 DTW为动态时间归整算法
用周平均的小时需求序列作为需求模式。另外，用graph embedding的方法(LINE)为每个结点构建一个嵌入向量m^i,再加入全连接层 :
\hat m^i=f(w_{fe} m^i+b_{fe})
预测组件
将Local CNN 以及 LSTM 的输出组合起来：
q_t^i=\hat m^i ⊕ h_t^i
并定义最终预测函数：\hat y_{t+1}^i=σ(W_{ff} q_t^i+b_{ff} )
其中w_{ff}与b_{ff}为训练参数。
损失函数
将上一步输出传入损失函数中：
L(θ)=\sum\limits_{i=1}^N((y_{t+1}^i-\hat y_{t+1}^i)^2+γ(\frac{y_{t+1}^i-\hat y_{t+1}^i}{y_{t+1}^i })^2)
其中θ为可学习参数，γ为超参数
mean square error更倾向于较大数值的预测，为了解决这个问题，加入了最小化mean absolute percentage loss
3.实际训练过程
13行Eq.9即损失函数
实验
2017年2月1日—2017年3月19日训练，3月20日—3月26日预测，取半小时/一小时时间间隔，预测时取前8小时数据预测后续几个时间片的数据
“There are 20x20 regions in our data. The size of each region is 0.7km x 0.7km”
评估函数：
“We use Mean Average Percentage Error (MAPE) and Rooted Mean Square Error (RMSE) to evaluate our algorithm”
MAPE=\frac{1}{ξ}\sum\limits_{i=1}^ξ\frac{(\hat y_{t+1}^i-y_{t+1}^i)}{(y_{t+1}^i )}
RMSE=\sqrt{\frac{1}{ξ}=\sum\limits_{i=1}^ξ(\hat y_{t+1}^i-y_{t+1}^2)^2}
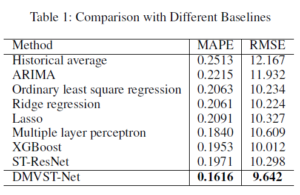
算法对比：
Historical average、ARIMA、LR、MLP、XGBoost、ST-ResNet
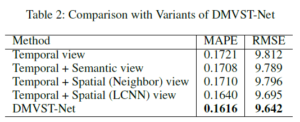
组合对比：
Temporal view、Temporal view+Semantic view、Temporal view+Spatial(Neighbors) view、Temporal view+Spatial(LCNN) view、DMVST-Net
对比结果
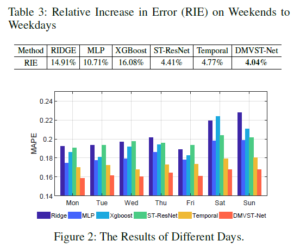
可以看出，在不同的方法、时间下，该模型都有着很好的效果。
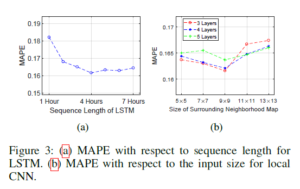
图四是对t长度、CNN层数进行效果实验
部分参数上处理的细节这里暂且不表，本文旨在介绍文章思路，有兴趣者可参考原文。
“一周一篇好论文” 是Master X对一些缺乏参考资源，自己感兴趣的论文进行个人向的翻译与解析的板块。
本栏目旨在起到分享、交流的作用（所以一周只是个象征性的时间量词，又没说每周嘛XD），为避免主观诱导点到为止。
文章著作权归Master X所有，转载请注明出处。
文章评论