Delayed Impact of Fair Machine Learning

本文发表于ICML，并获得了ICML 2018最佳论文奖，文章探究了机器学习中不同标准下对公平性的标准评估，提出并分析了不同标准下的公平性带来的结果。

全文较长，分为主体讨论与定理证明的附页，文章具有一定的文学性，内容紧凑，证明普遍易懂。为防割裂，这里只做主体讨论中的主要内容。

原文地址：立即下载

前言

机器学习的公平性主要是在静态分类环境中研究的，而不关心决策如何随时间而改变基础样本。传统观点认为，公平标准促进了它们旨在保护的群体的长期利益。

我们研究了静态公平标准如何与幸福感的时间指标相互作用，如感兴趣的利益变量的长期改善、停滞和下降。我们证明，即使在一步反馈模型中，一般的公平标准也不会随着时间的推移而促进改善，而且在不受约束的目标的情况下不仅不会带来改进，还可能会造成损害。我们完整地描述了三个标准的延迟影响，并对比了它们所表现出的不同性质的机制。此外，我们发现一种自然形式的测量误差扩大了公平标准表现良好的机制。

我们的结果强调了度量和时间建模在公平标准评估中的重要性，提出了一系列新的挑战和权衡取舍。

背景设置

文章分析到公平性的标准变化，是基于考虑到了历史遗留评价对弱势群体的影响的条件（例如，起初一些缺乏信用的群体开始很难借贷，而借贷次数减少反过来又导致信用下降），这样的公平标准自然符合人们的直觉，但缺乏对这样效果的严格论证。同时作者意识到上述变化并不总是向有益的方向。为了论证这点，作者以借贷为例，将客户分为两组，每个用户有信用评分并且每组分布不同（即存在弱势群体）。银行给用户放贷，好的情况下用户信用上升、银行利润增加，反之则相反。基于这种情境下作者提出了三种公平决策：

接着，作者开始数值化需要的数据。首先对于两组A、B，定义它们分别占人数比例为 gA 、 (1-gB) ，它们的评分分布分别为 πA、 πB ，每个评分的数值都属于有限集X。那么银行的不同决策可以看作τ A, τ B : X → [0, 1]。对于不同组j ∈ {A, B}，定义银行的效益为µ，那么我们所要研究的就是平均期望差∆µ_j。定性的话，我们可以区分长期改善(∆µ_j>0),停滞(∆µ_j= 0),和下降(∆µ_j< 0)。将之前的公平决策标号并研究。

本文贡献

表明了人口均等、最初机会均等等公平标准可以为弱势群体带来任何可能的结果，包括改善、停滞或恶化。在一定情况下人口均等会导致下降而最初机会均等不会。而在温和假设下遵循最优无约束选择政策(如利润最大化)，永远不会给弱势群体带来恶化的结果(主动伤害)。

引入了结果曲线的概念，简洁并数值化地描绘了一种标准由于其他的情况

通过FICO信用评分数据的实验支持了理论预测。

考虑了硬公平约束的替代方案。

问题设置

在背景设置的基础上，我们可以定义总利益U可以表示为：

其中，当我们研究平均期望差时，公式可以写作：

这两个公式作者提供了3种情景，证明了它们不仅仅适用于放贷，而具有一定的泛用性。

接着我们开始研究3种策略的具体表示情况。

为了方便理解，我们可以先定义选择率β，其在各组的表示形式为：

同时定义最大阈值MaxUtil，即银行为了达到最大利益，当超过这个阈值时开始盈利。即当达到此值时∆µj = 0。

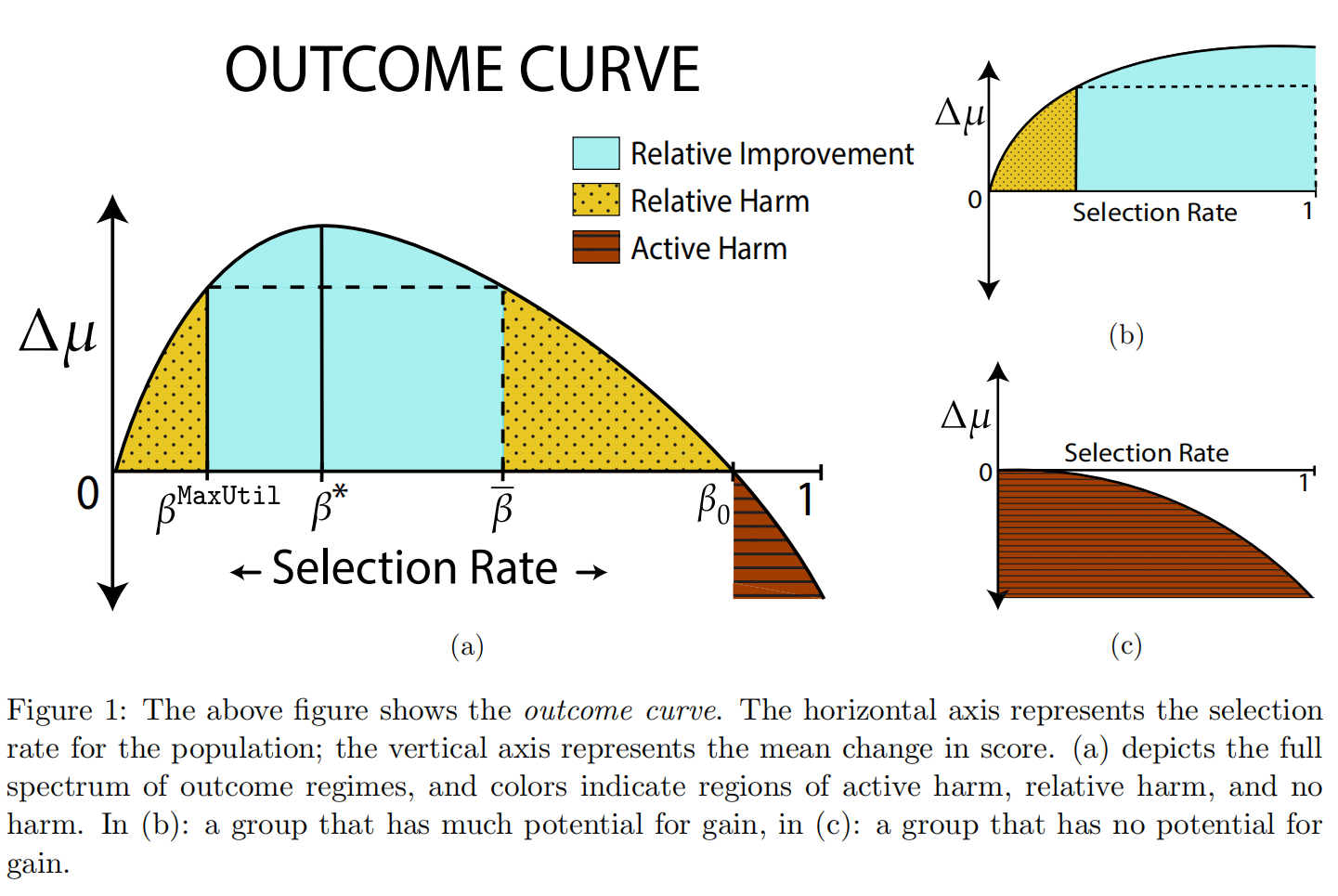
有了这两个定义，就可以画出结果曲线：

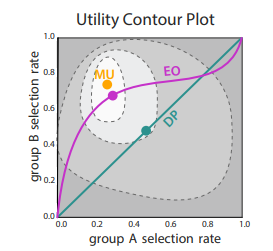
如图，横轴表示选择率，纵轴表示期望变化。阴影部分表示期望的各种变化情况（蓝色：改善，黄色：相对损害，棕色：下降）。由这3种情况定义了不同含义的选择率\beta^MaxUtil ，\beta_0 (一个经过计算可得到的分界)、\beta^* （峰值）、 \hat{\beta}（与MaxUtil相同时较大的取值）。

现在我们可以定义3种提及的公平准则了：

1)不受约束（MaxUtil）：即只考虑阈值取值和效益

2)人口均等（选择EqOpt）：定义真阳率：

TPR_j(\tau):=\frac{\sum_{x∈\chi}\pi_j(x)\rho(x)\tau(x)}{\sum_{x∈\chi}\pi_j(x)\rho(x)}

那么对于不同的 \beta_A 、\beta_B ，满足以下约束：

C={(\tau_A,\tau_B):TPR_A(\tau_A)=TPR_B(tau_B)}

作者构造了函数G^{(A→B)} 表示在TPR相同时B组的\beta 选择率\beta^'

结果分析

在这一部分，作者给出了众多推论及其详细证明，我们选取其中与本文贡献直接相关的部分来讲，具体证明简单阐述或写在后文。

首先确定定理一：MaxUtil永远不会造成损失（由曲线和定义可知）

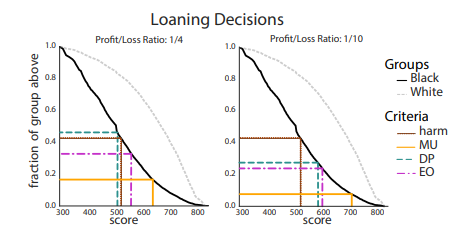
接着我们假设A组处于劣势，B组MaxUtil的接受率高于A组，根据3组策略不同作者通过实验绘制出了如下曲线：

由该图作者得到了以下几个推论：

1）（公平标准会造成相对提升）假设\beta_A^MaxUtil < \hat{\beta} 和 \beta_B^MaxUtil>\beta_A^MaxUtil ，那么存在群体比例g0<g1<1，使得对所有gA ∈ [g0, g1]，\beta_A^MaxUtil < \beta_A^DemParity < \hat{\beta}。即\beta_A^DemParity 会有相对提升。

证明：很好理解，相当于在图二中做一条垂直线使得MU<DP。

2）（公平标准会造成相对提升）假设存在 \beta_A^MaxUtil < \beta <\beta^‘ <\hat{\beta}  使得 \beta_B^MaxUtil > G^{(A→B)}(\beta) 、G^{(A→B)}(\beta^') ，那么存在群体比例g2<g3<1，使得对所有gA ∈ [g2, g3]， \beta_A^MaxUtil < \beta_A^EqOpt< \hat{\beta}， \beta_A^EqOpt即 会有相对提升。

证明：只是在证明1的基础上引入了真阳率的判断条件，注意转换即可。

3）（人口均等过度会造成损失）对于选择率 \beta，假设 \beta_B^MaxUtil > \beta>  \beta_A^MaxUtil。那么，存在比例g0使得对任意gA ∈ [0, g0]， \beta_A^DemPatity \beta 。特别地，当 \beta= \beta_0 时，DemPatity会造成损害；当 \beta= \hat{\beta}  时，DemPatity会造成相对损失。

证明：可以参考上一张outcome curve，相当于讨论不同的取值范围的可能性以及影响。

4）（机会相等过度会造成损失）假设\beta_B^MaxUtil>G^{(A→B)}(\beta) 且 \beta>\beta_A^MaxUtil。那么，存在比例g0使对任意gA ∈ [0, g0]，\beta>\beta_A^EqOpt。特别地，当 \beta>\beta_0时，EqOpt会造成损害；当\beta=\hat{\beta}  时，EqOpt会造成相对损失。

证明：同样的，可以参考上一张outcome curve，相当于讨论不同的取值范围的可能性以及影响。

接着作者比较了DemPatity和EqOpt。作者发现，这两种策略往往并不存在严格优劣关系。因此，作者给出了一种在满足一定期望条件下，EqOpt比DemPatity更好的情况。最后作者给出了一个三种标准结合分析的推论：

5）（DemPatity永远不会借贷少于MaxUtil，但EqOpt会）假设\beta_A^MaxUtil < \beta_B^MaxUtil且TPR_A(\tau^MaxUtil) >TPR_B(\tau^MaxUtil) ，那么 \beta_A^EqOpt<\beta_A^MaxUtil<\beta_A^DemPatity。也就是EqOpt会造成相对损失。

证明：即综上所有结论以及本图图一。

之后作者开始分析分布条件与MaxUtil的关系并引入了正规化因子，作者定义了一种放宽条件下的新分布，并结合之前的推论2，严格证明了新分布与原分布的选择率存在对应的大小关系。然后作者分析阈值与分布之间的关系，并最终得到了以下结论图：

并且作者将三种策略用在之前FICO数据下，得到了不错的结果。证实了在某些公平准则下反而会造成损失并给出了解释。

后续证明

作者在附页中针对几个常用的公式以及正规化的部分做了详细的证明说明，部分比较浅显易懂，这里只做出结论阐述。相比于这部分，前文中的三种策略的探究更能引起我的兴趣，有兴趣的同学可以自行研究。

展望与个人分析

这篇文章在文末给出了一些可能的分析方向，可做参考。

1.考虑超出群体平均变化影响的其他特征(如方差、个体水平结果)。

2.研究结果优化对建模和测量误差的鲁棒性

在我个人看来，这篇文章的优点在尽可能的条件下给出了非常详尽的情形分析与数学证明，站在数学角度上的详细分析本身就是一大创新点与亮点，并且行文紧凑，读来并不觉得乏味与疑惑。相比一类把玩公式变换、模棱两可的论文，此文一定程度上更有价值空间。

文章的缺点，或者应该说是可继续扩展研究的方向，我认为有以下几点：1.文章对于公平性的数学表示是一个二分性质的取舍函数，本文也提到是否有其他函数适用于其他或者更一般的情形呢？2.文章分析了CDF分布条件下的策略比较，是否可以比较其他一般化，甚至是一些不规则的分布？对于多组的情况又是否有其他变化？当然，除了文中提及的公平标准以及影响因素外，或许可以自己定义一种新的情景？

而从实际应用方向考虑，通过从公平性标准强加的约束转向结果建模，企业可能会开发出更有利可图、也“更公平”的系统，用于放贷或招聘，甚至可用于学校分配奖学金等。

“一周一篇好论文” 是Master X对一些缺乏参考资源，自己感兴趣的论文进行个人向的翻译与解析的板块。

本栏目旨在起到分享、交流的作用（所以一周只是个象征性的时间量词，又没说每周嘛XD），为避免主观诱导点到为止。

文章著作权归Master X所有，转载请注明出处。