[1] Group Equivariant Capsule Networks
Jan Eric Lenssen, Matthias Fey, Pascal Libuschewski
TU Dortmund University
这篇文章提出了组等变胶囊网络,该框架为胶囊网络引入了等效性和不变性。该工作有两个贡献点,首先,在每个组的元素上定义协议算法,提出通用路由,并证明了两种性质,即输出姿态向量的等效性和输出激活的不变性,在某些条件下保持不变。其次,将等变胶囊网络与来自群体卷积网络联系起来。
通过这种联系,作者们给出了两种方法具体如何相关,并且能够在一种深度神经网络架构中结合两种方法的优势。本文框架能够对组卷积运算符进行稀疏求值,能够控制特定等效性和不变性属性,在该框架中通过协议而不是池化操作来使用路由。
此外,该框架能够得到具有可解释和等变性的表示向量作为输出胶囊,从而将物体存在的证据从其姿势中分解出来。
组胶囊算法伪代码如下
稀疏组卷积及其正则图示如下
几种方法的效果比较如下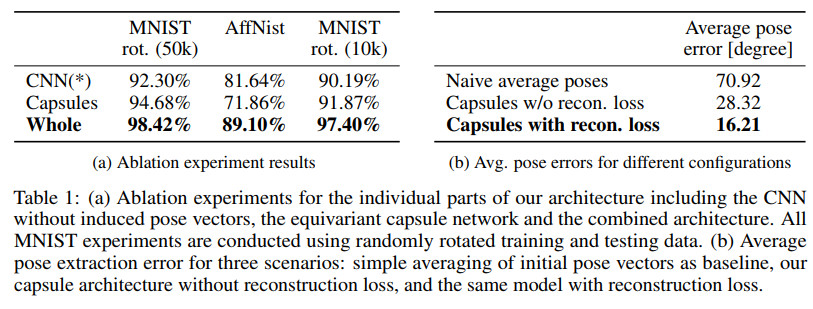
代码地址
https://github.com/mrjel/group_equivariant_capsules_pytorch
[2] Reversible Recurrent Neural Networks
Matthew MacKay, Paul Vicol, Jimmy Ba, Roger Grosse
University of Toronto
递归神经网络(RNN)处理序列数据时能够取得最佳性能,但是在训练时具有内存约束,这就限制了可训练RNN模型的灵活性。
在可逆RNNs中,隐含层到隐含层的转换可以反转,这能够减少训练所需存储量,因为这种RNNs中隐藏状态不需要存储,这些隐含状态在反向传播时能够重新计算。完全可逆的RNN,不需要存储隐含层的激活状态,但是由于不能忘记隐含层状态的信息,这就使得可逆RNN从根本上受到限制。
虽然如此,作者们提出一种存储少量位的方案,使得RNNs在遗忘隐含层状态的情况下也能实现完美的反转。本文所提出的方法能够取得跟传统模型相当的性能,同时将隐含层的激活状态内存成本降低为原来的1/15-1/10。
本文方法可以扩展到基于注意力的序列到序列模型,在保持性能的前提下,同时能够将编码器中隐含层激活状态所需存储成本降低为原来的1/10-1/5,在解码器中降低为原来的1/15-1/10。
模型图示如下
完全可逆乘法伪代码如下
神经翻译机的注意力图示如下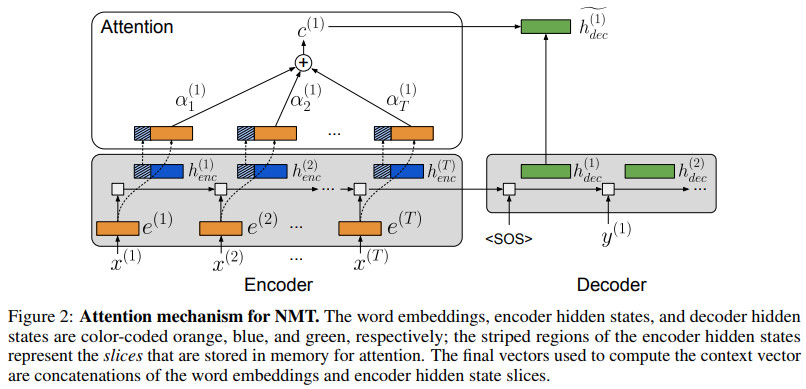
在数据集Penn TreeBank上的效果对比如下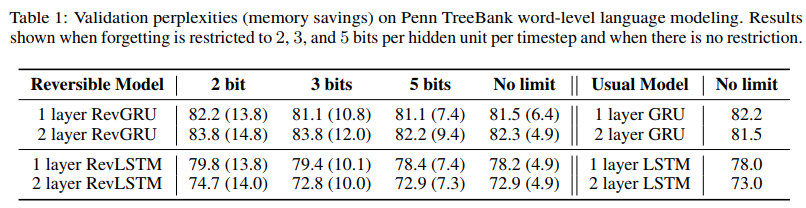
在数据集WikiText-2上的效果对比如下
在数据集Multi30K上的效果对比如下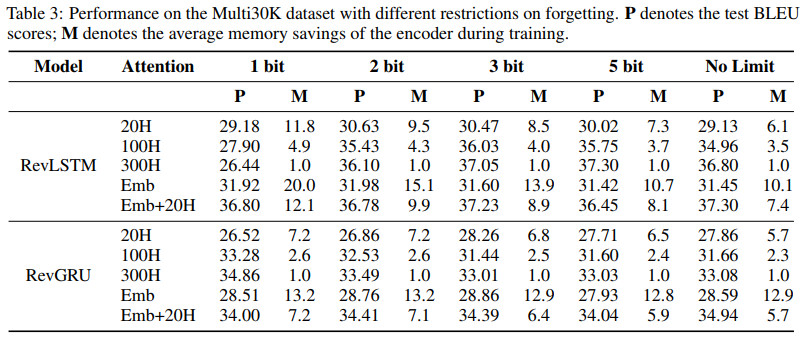
代码地址
https://github.com/matthewjmackay/reversible-rnn
[3] Deep Dynamical Modeling and Control of Unsteady Fluid Flows
Jeremy Morton, Freddie D. Witherden, Antony Jameson, Mykel J. Kochenderfer
Stanford University, Texas A&M University
控制流体流动的方程是非线性的,因此如何设计适当的流量控制系统仍然是一个挑战。但是, 计算流体力学 (CFD) 的最新进展表明,对复杂流体流动进行模拟能够得到较高的精度, 该研究促使了使用基于学习的方法来促进控制器的设计具有一定的可行性。
这篇文章提出了一种方法,即如何直接从 CFD 数据中学习气缸上气流的强迫和非强迫动力学。该方法基于 Koopman 理论,并且可以产生稳定的动力学模型, 进而可以预测气缸系统在扩展的时间范围内的时间演化过程。
利用所学到的动力学模型进行模型预测控制, 能够得到一个简单的、可解释的抑制气缸后涡旋脱落的控制律。
训练深层Koopman动力模型的结构图示如下
模型的输入形式图示如下
几种方法的效果对比如下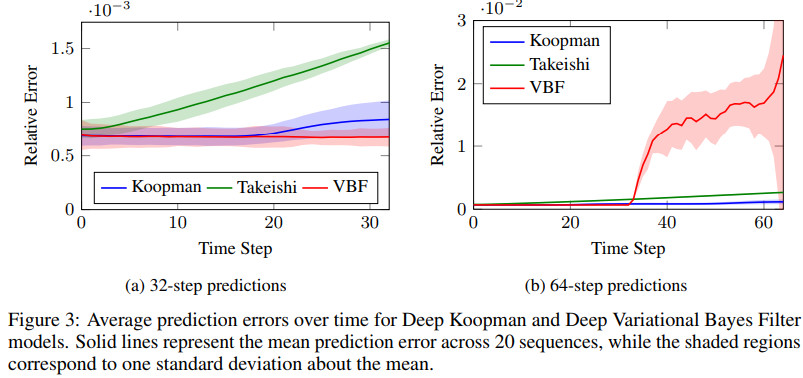
代码地址
https://github.com/sisl/deep_flow_control

文章评论